5、　 命题“在一个三角形中，等边对等角”的题设：___________________________，结论：__________________________.

4、　 2004年年初，在我国周边国家和我国部分地区发生了禽流感。禽流感病毒的病毒呈球状，杆状或丝状，其最小直径为80纳米，1纳米=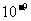，用科学记数法表示80纳米=_________米。

3、　 已知在⊙O中，弦AB的长为8㎝，圆心O到弦AB的距离为3㎝，则⊙O的半径是______________㎝.

2、　 若-1是方程的一个根，则k=___________

1、　 当x＝_______时，分式有意义。

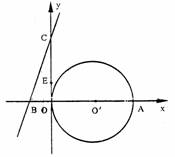
25．(本题满分11分)在平面直角坐标系中，点O′的坐标为(2，0)，⊙O′与x轴交于原点0和点A，又B、C、E三点的坐标分别为(－1，0)、(0，3)、(0，b)，且0<b<3．

　　 (1)求点A的坐标和直线BC的解析式；

　　 (2)当点E在OC上移动时，直线BE与⊙O′有哪几种位置关系?并求出每种位置关系时b的取值范围。

24．(本题满分11分)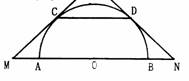己知：如图，AB是半圆O的直径，弧AC与弧BD相等，直线CM、DN分别切半圆于点C、D，且分别和直线AB相交于点M、N

(1)MO与NO相等吗?为什么?

(2)若∠M＝30°，试探索线段MN和线段CD的关系．

23．(本题满分10分)在数学里，我们规定：a^－n＝ (a≠O)．无论从仿照同底数幂的除法公式来分析，还是仿照分式的约分来分析，这种规定都是合理的．正是有了这种规定，指数的范围由非负数扩大到全体整数，概念的扩充与完善使我们解决问题的路更宽了．例如a²·a^－3＝a^2+(－3)＝a^－1＝。数的发展经历了漫长的过程，其实人们早就发现了非实数的数．人们规定：i²＝－1，这里数i类似于实数单位1，它的运算法则与实数运算法则完全类似：2i+i＝i(注意：由于非实数与实数单位不同，因此像2+i之类的运算便无法继续进行，2+i就是一个非实数的数)，6·0.5i＝3i; 2i·3i＝6i²＝－6；(3i)²＝－9;－4的平方根为±2i；如果x²＝－7，那么x＝±i．…数的不断发展进一步证实，这种规定是合理的．

(1)想一想，作这样的规定有什么好处?

　　 (2)试用配方法求一元二次方程x²+x+1＝0的非实数解：

(3)你认为，在学习中，当面临一个新的挑战时，我们应如何面对?

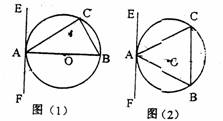
22、(本题10分)已知△ABC内接于⊙O，过点A作直线EF，(1)如图1，若AB为直径，要使得EF是⊙O的切线，还需要添加的条件是(只须写出两种不同情况)①＿＿＿＿＿＿＿＿＿＿＿＿＿或②＿＿＿＿＿＿＿＿＿＿。

(2)如图2，若AB为非直径的弦，∠CAE＝∠B，试说明EF是⊙O的切线。

21、(本题8分)(1)若｜x－1｜＝1－x。则x的取值范围是＿＿＿＿＿。

(2)在(1)的条件下，试求方程x²+｜x－1｜－3＝0的解。