2．下列式子中，从左到右的变形是因式分解的是(　　 )．

A．(x－1)(x－2)＝x²－3x+2　　 B．x²－3x+2＝(x－1)(x－2)

C．x²+4x+4＝x(x一4)+4　　 D．x²+y²＝(x+y)(x-y)

1．下列计算正确的是(　　 )

A．a·a²＝a²　 　B．(a²)²＝a⁴　 　C．a²·a³＝a⁶ 　　D．(a²b)³＝a²·b³

27．(10分)为了提高土地的利用率，将小麦、玉米、黄豆三种农作物套种在一起，俗称“三种三收”，这样种植的方法使成本不增加，且可将土地每亩的总产量提高40%，下表是这三种农作物单独种植时的亩产量、销售单价、种植成本的对应表：

现将面积为10亩的一块农田进行“三种三收”套种，为保证主要农作物的种植比例，要求小麦的种植面积占整个种植面积的一半。

(1)设玉米的种植面积为x亩，三种农作物的总销售价为y 元，写出y与x的函数关系式；

(2)在保证小麦种植面积不变的情况下，玉米、黄豆的面积均不低于一亩，且两种农作物均以整数亩种植，三种农作物套种的种植亩数有哪几种种植方案？

(3)在(2)的种植方案中，采用哪种套种方案才能使销售总价最高？最高价是多少？

(4)在(2)的种植方案中，采用哪种方案才能使总利润最大？利润最大是多少？

(总利润=销售总价－总成本)

26．(10分)小张骑车往返于甲、乙两地，距甲地的距离y(千米)与时间x(小时)的函数图象如图所示，

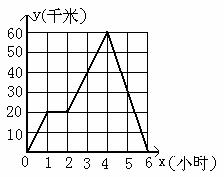(1)小张在路上停留　　　 小时，他从乙地返回时的速度是　　　　 千米/小时；

(2)小李与小张同时从甲地出发，按相同路线匀速前往乙地，到乙地停止，途中小李与小张共相遇3次，请在图中画出小李距甲地的距离y(千米)与时间x(小时)的函数大致图象；

(3)小王与小张同时出发，按相同路线前往乙地，小王离甲地的距离y(千米)与时间x(小时)的函数关系式为y=12x+10，小王与小张在途中共相遇几次？请你计算出第一次相遇的时间。

25．(6分)如图，△ABC为等边三角形，D、E为AC和BC边上的两点，且CD=CE，连接ED并延长到F，使AD=DF，连接AF、BD、CF，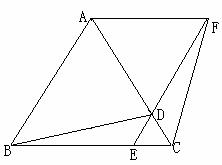

(1)写出图中所有全等的三角形(不加字母和辅助线)；

(2)从(1)中选一对全等三角形，说明全等的理由．

24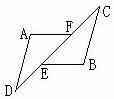．(6分)如图，在△ADF和△BCE中,∠A=∠B,点D、E、F、C在同一条直线上,有如下三个关系式:　①AD=BC　 ②DE=CF　 ③BE∥AF,

(1)请用其中两个关系式作为条件,另一个作为结论写出所有你认为正确的命题(用序号写出命题的形式,如:如果××,那么×)

(2)选择(1)中你写的一个命题,说明它正确的理由.

23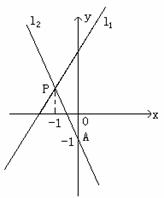．(4分)如图，l₁与l₂相交与点P，l₁的解析式为y=2x+3，点P的横坐标为－1，且l₂交y轴于点A(0，－1)，求l₂的解析式．

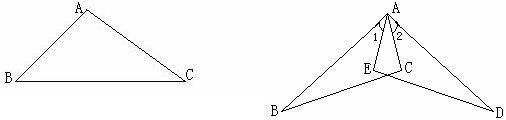
22．(4分)如图，AB=AD，AE=AC，∠1=∠2，求证：BC=DE

21．(4分)张老汉有四个儿子，张老汉想把如图所示的一块三角形地平均分给四个儿子种植，请你设计两种不同的方案(在已给的图形中直接画图，保留作图痕迹，不写作法)．

20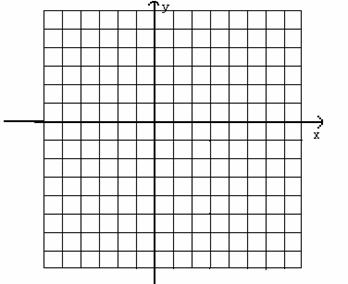．(6分)在所给的平面直角坐标系中画出函数y=－2x+2的图象，并根据图象回答问题：

(1)当x=－1时，y的值；

(2)当x为何值时，y＞0？

(3)若0≤x≤3，求y的取值范围？