9.选择因式分解方法的原则是:先看能否提公因式.在没有公因式的情况下:二项式用平方­差公式或立方和差公式,三项式用十字相乘法(特殊的用完全平方公式),三项以上用分­组分解法.注意:因式分解要进行到每一个多项式因式都不能再分解为止.

8.乘法公式(反过来就是因式分解的公式):①(a+b)(a－b)=a²－b².②(a±b)²=a²±2ab+b².③­(a+b)(a²－ab+b²)=a³+b³.④(a－b)(a²+ab+b²)=a³－b³;a²+b²=(a+b)²－2ab,(a－b)²=(a+b)²－4ab.

7.幂的运算性质:①­a^m×aⁿ=a^m+n.②a^m÷aⁿ=a^m－n.③(a^m)ⁿ=a^mn.④(ab)ⁿ=aⁿbⁿ.⑤(­ ­)ⁿ=­n­.⑥a^－n=n,特别:(­ ­)^－n=(­ ­)ⁿ.­⑦­a⁰=1(a≠0).

如:a³×a²=a⁵,a⁶÷a²=a⁴,(a³)²=a⁶,(3a³­)³=27a⁹,(－3)^－1=－­ ­,5^－2=­ ­=­ ­,­( ­)^－2=(­ ­)²=­ ­,(－3.14)⁰=1,­(­ ­－­ ­)⁰=1.

6.整式的乘除法:①几个单项式相乘除,系数与系数相乘除,同底数的幂结合起来相乘除.②单项式乘以多项式,用单项式乘以多项式的每一个项.③多项式乘以多项式,用一个多­项式的每一项分别乘以另一个多项式的每一项.④多项式除以单项式,将多项式的每一项

­分别除以这个单项式.

5.被开方数的小数点每移动2位,算术平方根的小数点就向相同方向移动1位;被开方数的­小数点每移动3位,立方根的小数点就向相同方向移动1位.

如:已知­ ­=0.4858,­则­ ­=­48.58;­已知 ­=1.558,则­ ­=­0.1588.

4.把一个数写成±a×10ⁿ­的形式(其中1≤a<10,n是整数),这种记数法叫做科学记数法.

­如:－40700=－4.07×10⁵,0.000043=­4.3×10^－5.

3.一个近似数,从左边笫一个不是0的数字起,到最末一个数字止,所有的数字,都叫做这个­近似数的有效数字.如:0.05972精确到0.001得0.060,结果有两个有效数字6,0.

2.　 ­绝对值:a≥0­ ­丨a丨=a;­a≤0­ ­丨a丨=－a.

如:丨－­ ­丨=­ ­;丨3.14－π丨=π－3.14.

1.　 整数(包括:正整数、0、负整数)和分数(包括:有限小数和无限环循小数)都是有理数.

如:－3,­ ­,0.231,0.737373…,­ ­,­ ­.­无限不环循小数叫做无理数..­如:π,－ ­,0.1010010001…(两个1之间依次多1个0).有理数和无理数统称为实数.

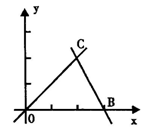
27．(12分)如图，直线OC、BC的函数关系式分别是y₁=x和y₂=-2x+6，动点P(x，0)在OB上运动(0<x<3)，过点P作直线m与x轴垂直．

　 (1)求点C的坐标，并回答当x取何值时y₁>y₂？

　 (2)设△COB中位于直线m左侧部分的面积为s，求出s与x之间函数关系式．

　 (3)当x为何值时，直线m平分△COB的面积？