
2、关于方程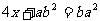 移项正确的是( )
A.
移项正确的是( )
A.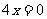 B.
B.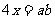
C.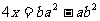 D.
D.
1、│-3│的绝对值是( )
A.3 B.-3 C.±3 D.0和-3
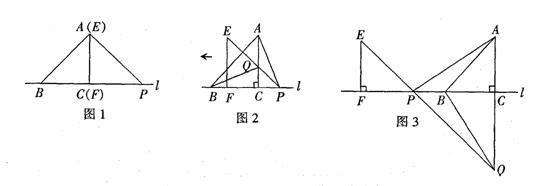
28.如图1,△ABC的边BC直线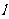 上,AC⊥BC,且AC=BC;△EFP的边FP也在直线
上,AC⊥BC,且AC=BC;△EFP的边FP也在直线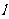 上,边EF与边AC重合,且EF=FP.
上,边EF与边AC重合,且EF=FP.
(1)在图1中,请你通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系;
(2)将△EFP沿直线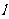 向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.猜想并写出BQ与AP所满足的数量关系和位置关系,请证明你的猜想;
向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.猜想并写出BQ与AP所满足的数量关系和位置关系,请证明你的猜想;
(3)将△EFP沿直线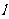 向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ.你认为(2)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.
向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ.你认为(2)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.




27.快乐公司决定按如图所示给出的比例,从甲、乙、丙三个工厂共购买200件同种产品A.已知这三个工厂生产的产品A的优等品率如表所示.
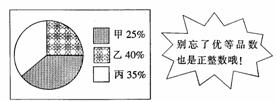
|
|
甲 |
乙 |
丙 |
|
优等品率 |
80% |
85% |
90% |
(1)快乐公司从甲厂购买____________件产品A;
(2)快乐公司购买的200件产品A中优等品有____________件;
(3)根据市场发展的需要,快乐公司准备通过调整从三个工厂所购买的产品A的比例,提高所购买的200件产品A中的优等品的数量.
①若从甲厂购买产品A的比例保持不变,那么应从乙、丙两工厂各购买多少件产品A,才能使所购买的200件产品A中优等品的数量为174件;
②你认为快乐公司能否通过调整从三个工厂所购买的比例,使所购买的200件产品A中优等品的数量为177件.若能,请问应从甲厂购买多少件产品A;若不能,请说明理由.
(本小题满分9分)
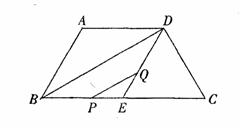
26.如图,梯形ABCD中,AD∥BC,AB=DC=AD=4,BD⊥CD,E是BC的中点.
(1)求ADBC的度数;
(2)求BC的长;
(3)点P从点B出发沿B→C以每秒3个单位的速度向点C匀速运动,同时点Q从点E
出发沿E→D以每秒1个单位的速度向点D匀速运动,当其中一点到达终点时,另一点也停止运动.设运动时间为t(s),连结PQ.当t为何值时△PEQ为等腰三角形.
(本小题满分9分)
|
分数段 (分) |
49.5- 59.5 |
59.5- 69.5 |
69.5- 79.5 |
79.5- 89.5 |
89.5- 99.5 |
|
频数 |
a |
9 |
10 |
14 |
5 |
 频率 频率 |
0.050 |
0.225 |
0.250 |
0.350 |
b |
(本大题共2小题,每小题8分,满分16分)
25.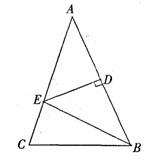 如图,在△ABC中,AB=AC,过腰AB的中点D作AB的垂线,交另一腰AC于E,连结BE.
如图,在△ABC中,AB=AC,过腰AB的中点D作AB的垂线,交另一腰AC于E,连结BE.
(1)若BE=BC,求∠A的度数;
(2)若AD+AC=24cm,BD+BC=20cm.求△BCE的周长.
24.七(3)班学生参加学校组织的“绿色奥运”知识竞赛,老师将学生的成绩按10分的组距分段,统计每个分数段出现的频数,填入频数分布表,并绘制频数分布直方图.
(1)频数分布表中a=___________,b=_____________;
(2)把频数分布直方图补充完整;
(3)学校设定成绩在69.5分以上的学生将获得一等奖或二等奖,一等奖奖励作业本15本及奖金50元,二等奖奖励作业本10本及奖金30元.已知这部分学生共获得作业本335本,请你求出他们共获得的奖金.
23.已知x+2y=5,xy=1.求下列各式的值
(1)2x2y+4xy2 (2)(x2+1)(4y2+1)
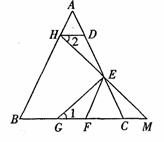
22.如图,在△ABC中,AB=AC,DE=EC,DH∥BC,EF∥AB,HE的延长线与BC
的延长线相交于点M,点G在BC上,且∠1=∠2.不添加辅助线,解答下列问题:
(1)找出图中的等腰三角形(不包括△ABC)____________________________;
(2)与△EDH全等的三角形有______________________________;
(3)证明:△EGC≌△EMF.
(本大题共2小题,每小题7分,满分14分)
21.如果二元一次方程组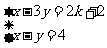 的解适合方程3x+y=-12,求k的值.
的解适合方程3x+y=-12,求k的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com