
2、创设情境 实验探究
要研究随机事件的概率,抛掷硬币的试验既典型又方便,但如果教师简单直叙说要抛掷硬币,难免让学生觉得被老师牵着走,兴趣不大。在这里,我借助于学生具有的课外知识--对世界杯的了解,让学生先看到世界杯的冠军奖杯,自然想到今年德国世界杯足球比赛,再给一幅图,让学生猜想到这是在由抛掷硬币决定哪个队先开球。然后,顺势提问:这种决定方法对比赛双方公平吗?为什么?
这个问题,问到了学生的心坎上,直觉判断:公平。可是,为什么呢?学生暂时答不上来。怎么办?能否用试验来验证?学生颇感怀疑。
无独有偶,历史上有几位著名的数学家都做过这样的试验,我们今天抛掷的结果会与他们一致吗?
第一步:分组试验
将全班分十组,要求每组掷一枚硬币60次,并把试验数据记录在表格中。
分析试验结果:
提问①:各小组正面朝上的频率一样吗?是否为0.5?
提问②:如果把全班十组结果进行累计,正面朝上的频率会有什么规律?
设计意图:
通过提问1:引导学生认识到随机事件的发生具有偶然性。
通过提问2:引导学生发现在次数逐渐增大的情况下,频率数值渐趋稳定。
第二步:比较试验
|
试验者 |
抛掷次数(n) |
正面向上的 次数(频数m) |
频率( ) ) |
|
棣莫弗 |
2048 |
1061 |
0.5181 |
|
布丰 |
4040 |
2048 |
0.5069 |
|
费勒 |
10000 |
4979 |
0.4979 |
|
皮尔逊 |
12000 |
6019 |
0.5016 |
|
皮尔逊 |
24000 |
12012 |
0.5005 |
这个表让学生既了解到一些数学家的故事、感受到他们为追求真理而不惜时间的精神(比如:皮尔逊投了24000次,可想而知需要大量时间),又惊喜的看到:几位数学家的试验结果跟我们今天的试验结果大致相同----大量试验次数下频率数值稳定于0.5。学生很有成就感,老师趁此鼓励:今天,你们就可以做出数学家做的事,那么明天,你们就是未来的数学家。
第三步:模拟试验
输入次数,电脑很快地抛掷硬币,得到正面朝上的频数和频率,并同时画出了频率随试验次数增大的曲线图。
学生一方面惊叹于信息技术为数学研究带来的方便(像这样的抛掷硬币,省时省力、直观形象),另一方面认识到:尽管是随机试验,尽管每一次事件的发生具有偶然性,但随着试验次数的增加,正面朝上的频率曲线越来越平稳:即稳定于0.5。
以上分三步实施的试验说明:“正面向上”的频率稳定于0.5,“反面向上”的频率也稳定于0.5。由两个频率稳定到的常数相等说明两者发生的可能性相等,从而验证了猜想,判断公平的直觉是对的。
到这时,学生已经看到,大量重复试验下,任意抛掷硬币“正面朝上”这个随机事件发生的频率逐渐稳定到的常数刻画了随机事件发生的可能性的大小。
为达到上述教学目标,教学中,我设置五个教学环节(见流程图)。
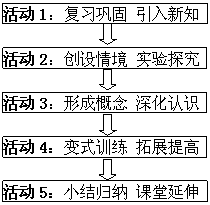
下面我重点谈谈整个教学过程:
1、复习巩固 引入新知
多媒体展示图片和问题:下列事件中,哪些是随机事件,哪些是必然发生的,哪些是不可能发生的。通过生动的实物图片和生活情境,一方面突出复习随机事件的判断,另一方面,可引出本节课的中心问题:随机事件发生的可能性有多大呢?如(遇上红灯、生个儿子、天气晴好)。自然地把学生引入到随机事件的概率的探究过程中来。
根据背景分析和学生的认知特点,我将本节课的教学目标设置为:
知识技能:
1)理解概率的含义并能通过大量重复试验确定概率。
2)能用概率知识正确理解和解释现实生活中与概率相关的问题。
过程方法:
1)经历用试验的方法获得概率的过程,培养学生的合作交流意识和动手能力。
2)在由“试验形成概率的定义”的过程中培养学生分析问题能力和抽象思维能力。
情感态度与价值观:
1)利用生活素材和数学史上著名例子,激发学生学习数学的热情和兴趣。
2)结合随机试验的随机性和规律性,让学生了解偶然性寓于必然性之中的辩证唯物主义思想。
2、学情分析:
1)、学生初学概率,面对概率意义的描述,他们会感到困惑:概率是什么,是否就是频率?因此辩证理解频率和概率的关系是教学中的一大难点。
2)、由于本节课内容非常贴近生活,因此丰富的问题情境会激发学生浓厚的兴趣,但学生过去的生活经验会对这节课的学习带来障碍,因此正确理解每次试验结果的随机性与大量随机试验结果的规律性是教学中的又一大难点。
1、教材分析:
按照教学内容交叉编排、螺旋上升的方式,本章是在统计的基础上展开对概率的研究的,而本节又是从频率的角度来解释概率,其核心内容是介绍实验概率的意义,即当试验次数较大时,频率渐趋稳定的那个常数就叫概率。本节课的学习,将为后面学习理论概率的意义和用列举法求概率打下基础。因此,我认为概率的正确理解和它在实际中的应用是本次教学的重点。
41.某商品的销售价为225元,利润率为25%,则该商品的进价为( D )
A、200元 B、250元 C、225元 D、180元
40.a,b是有理数,它们在数轴上的对应点的位置如下图所示:



 a 0
b
a 0
b
把a,-a, b, -b按照从小到大的顺序排列( C )
A. -b<-a<a<b B. -a<-b<a<b
C. -b<a<-a<b D. -b<b<-a<a
39.如果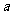 是有理数,则下列各式的值一定大于零的是( C )
是有理数,则下列各式的值一定大于零的是( C )
A、  B、
B、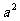 C、
C、 D、
D、
38.若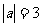 ,
, ,则
,则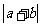 的值为( B ).
的值为( B ).
A、8 B、2 C、2或8 D、以上都不对
37、一个两位数,个位数字与十位数字的和是9,如果将个位数字与十位数字对调后所得新数比原数大9,则原来的两位数是 ( D )
A. 54 B. 27 C. 72 D. 45
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com