例3 (2006年成都市)计算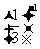：-+(-2)²×(-1)⁰-│-│．

　　 [点评]按照运算顺序进行乘方与开方运算。

[基础训练]

1．下列语句：①无理数的相反数是无理数；②一个数的绝对值一定是非负数；③有理数比无理数小；④无限小数不一定是无理数，其中正确的是(　 )

A．①②③　　 B．②③④　　 C．①②④　　 D．②④

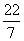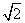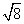例2　 下列实数、sin60°、、()⁰、3.14159、-、(-)^-2、中无理数有(　 )个

　　 A．1　　　 B．2　　　　 C．3　　　 D．4

[点评]对实数进行分类不能只看表面形式，应先化简，再根据结果去判断．

例1 ①a的相反数是-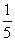,则a的倒数是_______．

②实数a、b在数轴上对应点的位置如图所示: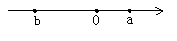

　　　 则化简│b-a│+=______．

③(2006年泉州市)去年泉州市林业用地面积约为10200000亩,用科学记数法表示为约______________________．

[点评]本大题旨在通过几个简单的填空，让学生加强对实数有关概念的理解．

2、　　 为了加强公民的节水意识，某市制定了如下用水收费标准：每户每月的用水不超过10吨时，水价为每吨1.2元；超过10吨时，超过的部分按每吨1.8元收费，该市某户居民5月份用水x吨(x >10)，应交水费y元，请用方程的知识来求有关x和y的关系式，并判断其中一个变量是否为另一个变量的函数？

1、小明去商店为美术小组买宣纸和毛笔，宣纸每张3元，毛笔每支5元，商店正搞优惠活动，买一支毛笔赠一张宣纸．小明买了10支毛笔和x张宣纸，则小明用钱总数y(元)与宣纸数x之间的函数关系是什么？

　　 过程：

　　 根据题意可知：

　　 当小明所买宣纸数x小于等于10张时，所用钱数为：y=5×10=50(元)

　　 当小明所买宣纸数x大于10张时，所用钱数为：y=50+(x-10)×3=3x+20(元)

　　 结果：

　　 当0<x≤10时　 y=50

当x>10时　　 y=3x+20

2、《课堂感悟与探究》

　Ⅵ．活动与探究

1、习题11．1．1－1、2、3、4题．

2．这个村人口数n是自变量，人均占有耕地面积y是n的函数．

函数关系式：y=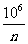

　Ⅳ．小结

　　 本节课我们通过回顾思考、观察讨论，认识了自变量、函数及函数值的概念，并通过两个活动加深了对函数意义的理解，学会了确立函数关系式、自变量取值范围的方法，会求函数值，提高了用函数解决实际问题的能力．

　Ⅴ．作业

1．正方形边长x是自变量，正方形面积S是x的函数．

　　 函数关系式：S=x2

2．秀水村的耕地面积是106m2，这个村人均占有耕地面积y随这个村人数n的变化而变化．

　　 解答：