3．用不等式表示:y的一半与5的和大于1. 答案:y／2+5＞1.——青夏教育精英家教网—

1．引导学生通过讨论完成对第54-55页的探索部分的内容，在此过程中提示学生把人数“x”看作一个数然后再考虑问题。
2．概括出不等式的描述性定义(课本第55页)，然后引导学生举出一些不等式的例子。
3．引入不等式的解的定义，并引导学生观察课本第55页的表格，让学生指出120＜5x的整数解，并思考不等式的解是否唯一。
4．通过讲解课本第56页例题(1)(2)，教会学生怎样从文字表述转化成不等式，并引导学生完成该例题的(3)(4)。
5．布置适当的练习。

1．认真思考，积极讨论，在教师的提示下，将x看作一个数，从而得到120＜5x这个不等式，并由表格中的x的值通过计算完成表格。
2．认真听讲，理解不等式的内涵，并能给出一些不等式的例子，举出了例子如：3x+5＜8；5y－7＞3。
3．通过教师的讲解，理解不等式的解的定义，结合表格找x＝25、26、27，是不等式120＜5x的解，并发现不等式的解不是唯一的。
4．认真听取教师讲解，明白如何用不等式表示不等量之间的关系，并通过讨论完成例题的后两个小题。
　
　
5．认真地完成练习，巩固所学。

　　本课总结

　　本节课借助生活的实例引入不等量的关系，进而使学生学习了用不等式表示这些等量关系，接着引入了不等式的相关概念，并鼓励学生分组讨论，对用不等式表达数量之间的关系有初步的认识。

　　板书设计

§ 13.1　认识不等式

试题详情

教师活动

学生活动

1．引导学生思考如下例题：已知a＜－1＜b＜0＜c＜1＜d，且|a+1|＝|b+1|，|1－c|＝|1－d|。求a+b+c+d的值。
引导学生考虑根据a、b、c、d的取值范围解决问题，组织学生讨论，并鼓励学生主动上台板演。
2．总结学生的板演并指出：本题的关键在于将几个变量看作一个整体。提醒学生注意这种解题方法。
3．引导学生讨论完成下面的例题：已知方程组的解x与y的和是正数，求a的取值范围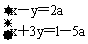

提示学生可以考虑用a表示x和y，并鼓励学生上台板演。
　
4．总结学生的答案，指出本题的重点在于是用了转化思想，并提醒学生注意本方法在以后学习中的应用。

1．认真思考，积极讨论，在教师的提示下发现：a+1＜0，b+1＞0所以|a+1|＝|b+1|等价于：－1－a＝1+b所以a+b＝－2。用相同的方法得到c+d＝2。于是有：a+b+c+d＝－2+2＝0。发现本题的解决关键在于将a+b和c+d看作整体。同时积极地上台板演。
2．认真听取老师的总结，体会将变量看作整体的方法。
　
3．认真思考，积极讨论，分析：方程组有三个未知数，不可能解出准确的解。既然本题要求的是a的取值范围，那么就用a来表示x和y，然后根据x+y的范围来确定a的范围。
通过解方程得到：x＝(1+a)／4；y＝(1-7a)／4，从而由x+y＞0得到：a＜1／3。积极地上台板演。
　
4．听取老师的总结，体会转化思想的作用。

试题详情

教师活动	学生活动
1．复习回顾不等式、一元一次不等式(组)及其解集的概念和解法，提示学生不必死记硬背，可以通过举例说明。 2．总结学生的发言，并将本章的内容作一次总结，指出本章重难点，鼓励学生作出知识结构图。 3．出示规范的知识结构图，指出本章的基础在于不等式性质的应用。	1．用自己的语言说出各种定义和方法，并举出实例。　 2．认真听讲，理清本章知识脉络，把握重难点，并根据自己的理解画出知识结构图。(可能画得不太全面) 3．对比教师给出的结构图，完善自己的知识结构，并认识本章的基础。

试题详情

3、在应用不等式式解决实际问题时，要注意从题意中分析得出不等关系。

试题详情

同步练习册答案

练习册

高中

初中

小学