
5.大伯出去散步,从家走了20分钟,到一个离家900米的阅报亭,看了10分钟报纸后,用了15分钟返回到家,下面哪个图形表示张大伯离家时间与距离之间的关系( ):
4.如图,直线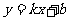 经过A(0,2)和B(3,0)两点,那么
经过A(0,2)和B(3,0)两点,那么
这个一次函数关系式是( )
A. B.
B.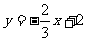 C.
C.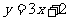 D.
D.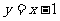
2.下列函数关系式:①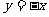 ;②
;②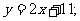 ③
③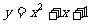 ;④
;④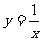 .其中一次函数的个数是( )
.其中一次函数的个数是( )
A. 1个 B.2个 C.3个 D.4个
 3.在直角坐标系中,既是正比例函数
3.在直角坐标系中,既是正比例函数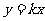 ,又是
,又是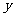 的值随
的值随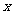 值的增大而减小的图像是( )
值的增大而减小的图像是( )
 A
B
C
D
A
B
C
D
1.判断下列变化过程中,两变量存在函数关系的是( )
A.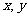 是变量,
是变量,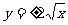 B.人的身高与年龄
B.人的身高与年龄
C.三角形的底边长与面积 D.速度一定的汽车所行驶的路程与时间.
2. 某服装厂现有A种布料70m,B种布料52m,现计划用这两种布料生产M、N两种型号的时装80套。已知做一套M型号的时装需要A种布料0.6m,B种布料0.9m,可获利45元,做一套N型号的时装需要A种布料1.1m,B种布料0.4m,可获利50元。若设生产N型号的时装套数为x,用这批布料生产这两种型号的时装所获的总利润为y元。
(1)求y与x的函数关系式,并求出自变量x的取值范围;
(2)该服装厂在生产这批时装中,当生产N型号的时装多少套时,所获利润最大?最大利润是多少?
1.如果把函数y=2x的图像向下平移两个单位,再向左平移 一个单位,那么得到的图像是
函数 的图像.
5.小强骑自行车去郊游,右图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象。小明9点离开家,15点回家,根据这个图象,请你回答下列问题:
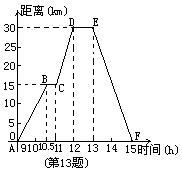 (1)小强到离家最远的地方需几小时?此时离家多远?
(1)小强到离家最远的地方需几小时?此时离家多远?
(2)何时开始第一次休息?休息时间多长?
(3)小强何时距家21km?(写出计算过程)
*附加题(第1题3分,第2题7分)
3. 利用函数图象求不等式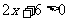 的解.
的解.
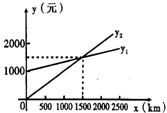
4某单位需要用车,准备和甲乙两个出租公司其中的一家签订合同,设汽车每月行驶xkm,应付给甲的月租费是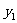 元,付给乙出租车公司的月租费是
元,付给乙出租车公司的月租费是 元,y分别与x之间的函数关系图象是如图所示的两条直线,观察图象,回答下列问题:
元,y分别与x之间的函数关系图象是如图所示的两条直线,观察图象,回答下列问题:
(1)每月行驶的路程等于多少时,租两家车的费用相同?
(2)每月行驶的路程在什么范围内时,租甲出租车公司比较合算?
(3)如果这个单位估计每月行驶的路程为2300km,那么这个单位租哪家的车合算?
2. 一台拖拉机工作时,每小时耗油6L,已知油箱中有油40L.
(1)设拖拉机的工作时间为t(h),油箱中的剩余油量为QL,求出Q(L)与t(h)之间的函数关系式.
(2)求出自变量的取值范围
(3)当油箱内剩余油10L时,这台拖拉机已工作了几小时?
1.已知一次函数图象经过(3,5)和 两点,(1)求此一次函数解析式;(2)若点(a,2)在函数图象上,求a的值。
两点,(1)求此一次函数解析式;(2)若点(a,2)在函数图象上,求a的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com