
1.判断下列变化过程中,两变量存在函数关系的是( )
A.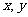 是变量,
是变量,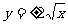 B.人的身高与年龄
B.人的身高与年龄
C.三角形的底边长与面积 D.速度一定的汽车所行驶的路程与时间.
17.(1)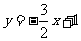 .(2)2.(3)
.(2)2.(3)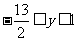 . 18.(1)A(
. 18.(1)A(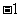 ,0),B(1,0),P(
,0),B(1,0),P(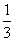 ,
,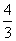 ).(2)
).(2)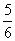 .(3)
.(3)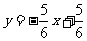 . 19.(1)5升.(2)
. 19.(1)5升.(2)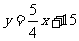 .(3)
.(3)
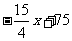 . 20.(1)
. 20.(1)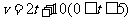 ,
,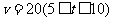 ,
,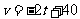 .(2)100米. 21.(1)
.(2)100米. 21.(1)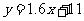 .(2)配套. 22.(1)8,4.(2)
.(2)配套. 22.(1)8,4.(2)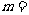 1,
1,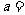 4,
4,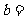 11.(3)
11.(3)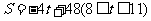 ,
,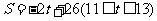 .
.
15.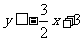 16.12
16.12
9.四 10.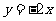 11.
11.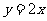 12.
12.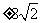 13.
13.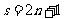 14.
14.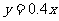
1.B 2.C 3.A 4.C 5.D 6.C 7.B 8.D
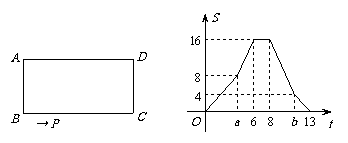
22.如图,长方形ABCD中,点P沿着四边按B→C→D→A方向运动,开始以每秒m个单位匀速运动,a秒后变为每秒2个单位匀速运动,b秒后恢复原速匀速运动.在运动过程中,△ABP的面积S与运动时间t的函数关系如图所示.
(1)求长方形的长和宽;
(2)求m、a、b的值;
(3)当P点在AD边上时,求S与t的函数解析式
 www.1230.org 初中数学资源网
www.1230.org 初中数学资源网
单元学习评价六(测试题)
21.为了保护学生的视力,课桌椅的高度都是按一定的关系配套设计的.研究表明:假设课桌高度为ycm,椅子的高度(不含靠背)为xcm,则y应是x的一次函数.下表列出两套符合条件的课桌椅的对应高度:
|
|
第一套 |
第二套 |
|
椅子高度x(cm) |
40.0 |
37.0 |
|
桌子高度y(cm) |
75.0 |
70.2 |
(1)请确定y与x的函数关系式;
(2)现有一把高42.0cm的椅子和一张高78.2cm的课桌,它们是否配套?为什么?
20.某汽车在20秒内运动的速度v与时间t的图象如图所示.
(1)写出速度v与时间t的函数关系式;
(2)求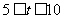 时汽车行驶的路程.
时汽车行驶的路程.
19.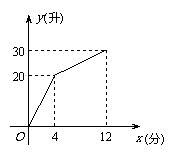 有一个附有进出水管的容器,每单位时间内进出的水量都是一定的.设从某时刻开始的4分钟只进水不出水,在随后的8分钟内既进水又出水,得到时间x(分)与水量y(升)之间的关系如图所示.
有一个附有进出水管的容器,每单位时间内进出的水量都是一定的.设从某时刻开始的4分钟只进水不出水,在随后的8分钟内既进水又出水,得到时间x(分)与水量y(升)之间的关系如图所示.
(1)每分钟进水多少?
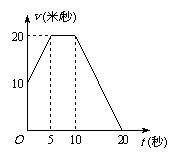
(2)当4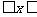 12时,x与y有何关系?
12时,x与y有何关系?
(3)若12分钟后,只放水不进水,求y的表达式.
18.如图,直线PA是一次函数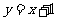 的图象,直线PB是一次函数
的图象,直线PB是一次函数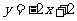 的图象.
的图象.
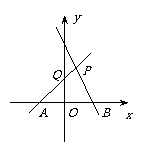 (1)求A、B、P三点的坐标;
(1)求A、B、P三点的坐标;
(2)求四边形PQOB的面积;
(3)若过B点的一条直线平分四边形PQOB的面积,
求这条直线的解析式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com