
3.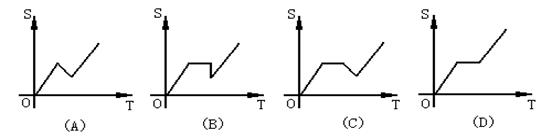 某人骑车沿直线旅行,先前进了
某人骑车沿直线旅行,先前进了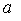 千米,休息了一段时间,又原路返回
千米,休息了一段时间,又原路返回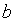 千米(
千米(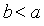 ),再前进
),再前进 千米,则此人离起点的距离S与时间t的关系示意图是( )。
千米,则此人离起点的距离S与时间t的关系示意图是( )。
2.已知一次函数Y=KX+b ,当x =0时,y <0;,当y =0时,x >0,那么下列结论正确的是
( )
|
A、k >0,b >0 |
B、k >0,b <0 |
C、k <0,b >0 |
D、k <0,b <0 |
1.直线y=3X+b 与两坐标轴围成的三角形面积为6,求与Y轴的交点坐标 ……………………………( )
|
A、(0,2) |
B、(0,-2) (0,2) |
|
C、(0,6) |
D、(0,6)、(0,-6) |
3.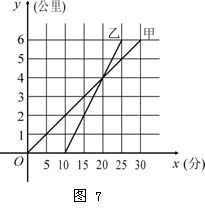 甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行 驶 过程中路程与时间的函数关系的图象如图7. 根据图象解决下列问题:
甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行 驶 过程中路程与时间的函数关系的图象如图7. 根据图象解决下列问题:
(1) 谁先出发?先出发多少时间?谁先到达终点?先到多少时间?
(2) 分别求出甲、乙两人的行驶速度;
(3) 在什么时间段内,两人均行驶在途中(不包括起点和终点)?在这一时间段内,请你根据下列情形,分别列出关于行驶时间x的方程或不等式(不化简,也不求解):① 甲在乙的前面;② 甲与乙相遇;③ 甲在乙后面.
2.某公司到果园基地购买某种优质水果,慰问医务工作者,果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案,甲方案:每千克9元,由基地送货上门。乙方案:每千克8元,由顾客自己租车运回,已知该公司租车从基地到公司的运输费为5000元。
(1)分别写出该公司两种购买方案的付款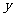 (元)与所购买的水果质量
(元)与所购买的水果质量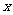 (千克)之间的函数关系式,并写出自变量
(千克)之间的函数关系式,并写出自变量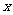 的取值范围。
的取值范围。
(2)依据购买量判断,选择哪种购买方案付款最少?并说明理由。
1. 在某地,人们发现某种蟋蟀1分钟所叫次数与当地温度之间近似为一次函数关系。下面是蟋蟀所叫次数与温度变化情况对照表:
|
蟋蟀叫次数 |
… |
84 |
98 |
119 |
… |
|
温度(℃) |
… |
15 |
17 |
20 |
… |
(1)根据表中数据确定该一次函数的关系式;
(2)如果蟋蟀1分钟叫了63次,那么该地当时的温度大约为多少摄氏度?
8. 根据下图所示的程序计算函数值,若输入的x值为 ,则输出的结果为 .
,则输出的结果为 .

7.若一次函数y=kx+b的图像经过(-2,-1)和点(1,2),则这个函数的图像不经过 象限 .
6.已知直线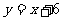 与
与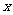 轴,
轴,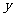 轴围成一个三角形,则这个三角形面积为 ________.
轴围成一个三角形,则这个三角形面积为 ________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com