
(一)、基本概念
1.函数的概念
一般地,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有惟一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
2.一次函数和正比例函数的概念
若两个变量x,y之间的关系式可以表示成y=kx+b(k,b为常数,且k≠0)的形式,则称y是x的一次函数(x是自变量).
特别地,当b=0时,称y是x的正比例函数.
19. (16分) 在直角坐标系中, 我们把横、纵坐标都为整数的点叫整点. 设坐标轴的单位长度为1厘米, 整点P从原点O出发, 速度为1厘米/秒, 且整点P作向上或向右运动(如图所示), 运动时间(秒)与整点(个)的关系如下表:
|
整点P从原点O出发的时间(秒) |
可以得到整点P的坐标 |
可以得到整点P的个数 |
|
1 |
(0, 1)、(1, 0) |
2 |
|
2 |
(0, 2)、(1, 1)、(2, 0) |
3 |
|
3 |
(0, 3)、(1, 2)、(2, 1)、(3, 0) |
4 |
|
…… |
…… |
…… |
根据表中的规律, 回答下列问题:
(1)当整点P从点O出发4秒时, 可以得到整点P的个数为______________个;
(2)当整点P从点O出发8秒时, 在直角坐标系中描出可以得到的所有整点, 并顺次连接这些整点;
(3)当整点P从点O出发_________秒时, 可到达整点(16, 4)的位置;
(4)当整点P(x, y)从点O出发30秒时, 整点P(x, y)恰好在y=2x-6上, 求整点P(x, y)的坐标.
静心想一想 (不计入总分)
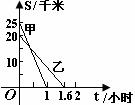
甲、乙两名同学同时从各自的家里去同一所学校, 他们距学校的路程S(千米)与行走的时间t(小时)之间的关系如图所示, 请根据图象所提供的信息解答下列问题:
(1)分别求出甲、乙两同学距学校的路程S(千米)与t(小时)之间的函数关系式;
(2)在什么时间, 甲、乙两同学距学校的路程相等? 在什么时间段内, 甲同学比乙同学离学校远? 在什么时间段内, 甲同学比乙同学离学校近?
18. (10分) 当m、n为何值时, y=(2m1)x5-2n +(n+m)是一次函数? 何值时为正比例函数?
17. (12分) 小明受故事《乌鸦喝水》的启发, 利用量桶和体积相同的小球进行了如下操作(如图):
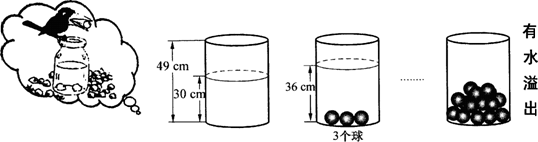
请根据图中给出的信息,解答下列问题:
(1)放入一个小球量桶中水面升高___________cm;
(2)求放入小球后量桶中水面的高度y(cm)与小球个数x(个)之间的一次函数关系式(不要求写出自变量的取值范围);
(3)量桶中至少放入几个小球时有水溢出?
16. 一次函数y=ax+b, 若a+b=8, 则图象必经过点___________________.
15. 一次函数y=ax+b与y=bx+a的图象如图所示.
一次函数y=ax+b与y=bx+a的图象如图所示.
(1)判断a与b的大小关系______________; (2)直线y=ax+b与y=bx+a的交点坐标为____________;
(3)当x__________时, ax+b<bx+a; 当x__________时, ax+b>bx+a.
14. 若一次函数y=(2-m)x+m的图象经过第一、二、四象限, 则m的取值范围是________________.
13. 一次函数y=-x+6的图象经过M(a, b)、N(c, d)两点.
(1)若a<c, 则b与d的大小关系是_________________________.
(2)代数式a(c+d)+b(c+d)的值为________________________.
12. 正比例函数y=3x与一次函数y=x+2图象的交点A的坐标是_______________, 如果一次函数与x轴交于点C, 与y轴交于点B, 则点B的坐标为_______________, 点C的坐标为________________, 原点为O, 则△AOC的面积为___________________, △AOB的面积为_________________.
11. 如图, 表示弹簧长度y(cm)与所挂物体的质量x(kg)(最多只能挂25kg的物体)之间的函数图象.
(1)根据图象提供的已知数据, 确定y与x之间的函数关系式是_________________________.
(2)自变量x的取值范围是_______________________
(3)当弹簧挂10kg的物体时, 弹簧长度为__________________cm.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com