
4、一次函数y=kx+b(k ≠ 0)的性质:
⑴当k>0时,y随x的增大而_________。
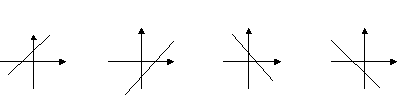 ⑵当k<0时,y随x的增大而_________。
⑵当k<0时,y随x的增大而_________。
⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图
|
k 0 ,b___0 k___0,b___0 k___0,b___0 k___0,b_
(通过做练习,回顾一次函数的相关知识,以达到巩固双基的目的)
3、正比例函数y=kx(k≠0)的性质:
⑴当k>0时,图象过______象限;y随x的增大而____。
⑵当k<0时,图象过______象限;y随x的增大而
2、一次函数y=kx+b(k≠0)的图象是过点(0,___) 的__________。
1、正比例函数y=kx(k≠0)的图象是过_________的 。
2.一次函数的图像与性质
1、一次函数的概念:函数y=_______(k、b为常数,k______)叫做一次函数。当b_____时,函数y=____(k____)叫做正比例函数。
★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次,
⑵、比例系数_____。
1. 函数的定义.
我们知道,一次函数在日常生活和生产实践中有着许多直接应用,你知道一次函数的哪些相关知识?今天,让我们一起来复习一次函数.
(从学生已有的知识经验入手,导入复习课,尊重学生的认知水平)
4.方程方法
方程方法是指对所求数学问题通过列方程(组)使问题得解的方法.在函数及其图象中,方程方法的应用主要体现在运用待定系数法确定函数关系式中.
例6 已知一次函数y=kx+b(k≠0)的图象经过点A(-3,-2)及点B(1,6),求此函数关系式,并作出函数图象.
(分析) 可将由已知条件给出的坐标分别代入y=kx+b中,通过解方程组求出k,b的值,从而确定函数关系式.
解:由题意可知,
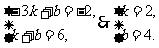
∴函数关系式为y=2x+4.
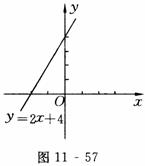
图象如图11-57所示.
[说明] 一次函数y=kx+b中含有两个待定系数k,b,根据待定系数法,只要列出方程组即可.
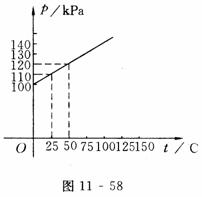
例7 科学家通过研究得出:一定质量的某种气体在体积不变的情况下,压强p(kPa)随温度t(℃)变化的函数关系式是p=kt+b,其图象如图11-58所示的直线.
(1)根据图象求出上述气体的压强P与温度t之间的函数关系式;
(2)当压强p为200kPa时,求上述气体的温度.
(分析) 要求出p与t之间的函数关系式,需知图象上的两个点的坐标,由图象可知,点
(25,110),(50,120)在该图象上,通过解方程可得关系式.
解:(1)观察图象可知,点(25,110),(50,120)在该图象上.
∴
∴函数关系式为p= t+100.
t+100.
(2)当p=200时,有
200= t+100,
t+100,
∴t=250.
∴当压强P为200kPa时,气体的温度是250℃.
3.分类讨论法
分类讨论法是在对数学对象进行分类的过程中寻求答案的一种思想方法.分类讨论法既是一种重要的数学思想,又是一种重要的教学方法.分类的关键是根据分类的目的,找出分类的对象,分类既不能重复,也不能遗漏,最后要全面总结.
例4 在一次遥控车比赛中,电脑记录了速度的变化过程,如图11-56所示,能否用函数关系式表示这段记录?
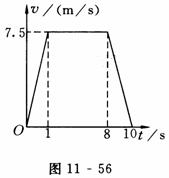
(分析)根据所给图象及函数图象的增减性,本题要分三种情况进行讨论.电脑记录提供了赛车时间t(s)与赛车速度υ(m/s)之间的关系,在10s内,赛车的速度从0加速到7.5m/s,又减至0,因此要注意时间对速度的影响.
解:观察图象可知,
当t在0-1s内时,速度υ与时间t是正比例函数关系,
υ=7.5t(0≤t≤1);
当t在1-8s内时,速度υ保持不变,
υ=7.5(1<t≤8);
当t在8-10s内时,速度υ与时间t是一次函数关系,
υ=-3.75t+37.5(8<t≤10=.

例5 某商场计划投入一笔资金采购一批紧俏商品,经过市场调查发现,如果月初出售可获利15%,并可用本利和再投资其他商品,到月末又可获利10%;如果月末出售可获利30%,但要付仓储费用700元,问他如何销售获利较多?
(分析)两种方式获利多少与投入资金有关,需要分类讨论,题中的三个百分比是对投资来讲的,设该商场投入资金x元,则按不同方式销售的获利情况:月初出售共获利15%x+(x+15%)·1O%;月末出售共获利3O%x-700.然后比较两种销售方式获利的多少.
解:设商场计划投资x元,在月初出售共获利y1元,在月末出售共获利y2元,根据题意,得
y1=15%x+(x+15%x)·10%=0.265x,
y2=30%x-700=0.3x-700.
∴y1-y2=0.265x-(0.3x-700)=700-0.035x.
①当y1-y2=0时,有700-0.035x=0,∴x=20000.
∵当x=20000时,两种销售方式获利一样多.
②当y1-y2>0时,有700-0.035x>0,∴x<20000.
∴当x<20000时,y1>y2.即月初出售获利较多.
③当y1-y2<0时,有700-0.035x<0,∴x>20000.
∴当x>20000时,y1<y2.即月末出售获利较多.
[说明]进行有关问题的分类讨论,要全面考察,可根据图形或题意找出所有可能的情况,然后进行总结.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com