1. 直线如图1所示，化简：　　　．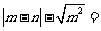

24．

25．

解：(1)当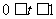时，设y与t的函数解析式为，由题意得，所以。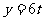

当时，设y与t的函数解析式为，则由题意得，解得

，所以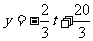，故y与t的函数解析式为．

(2) 当时，则由题意得，。当时，由题意得，解得，所以注射药液小时后开始有效，有效时间长为(小时)。

；22．设每周参观人数与票价之间的一次函数关系式为y＝kx+b．由题意得解得∴y＝－500x+12 000．根据题意,得xy＝40 000,即x(-500x+12 000)=40 000,x²-24x+80=0,即(x－12)²＝64，两边开平方解得x₁=20,x₂=4．把x₁=20,x₂=4分别代入 y=-500x+12 000中得y₁=2 000,y₂=10 000．因为控制参观人数,所以取x=20,y=2 000．答:每周应限制参观人数是2 000人,门票价格应是20元；

23．

17． 、；18．5；19．y＝－x+15；20．75．5．

25．(12分)为了抗击“禽流感”，医药工作者们经过不懈的研究，终于研制了一种新药，在临床试验时观察发现，如果成人按规定的剂量注射这种抗生素，注射药液后每毫升血液中含药量y(微克)与时间t(小时)之间的关系近似地满足如图所示的折线。

(1)写出注射药液后每毫升血液含量y与时间t之间的函数解析式及自变量的取值范围。

(2)据临床观察：每毫升血液中含药量不少于4微克时，控制病情是有效的。如果病人按规定的剂量注射该药液后，那么这一次注射的药液经过多长时间后控制病情开始有效？这个有效时间有多长？

答案D卷：

24．(12分)甲、乙两辆汽车在一条公路上匀速行驶，为了确定汽车的位置，我们用数轴表示这条公路，原点O为零千米路标，如图(1)所示，并作如下约定：(1)速度v＞0，表示汽车向数轴正方向行驶；速度v<0,表示汽车向数轴负方向行驶；速度v=0，表示汽车静止；(2)纵坐标s>0，表示汽车位于原点右侧；纵坐标s<0，表示汽车位于原点左侧；纵坐标s=0，表示汽车位于原点，遵照上述约定，将这两辆汽车在公路上匀速行驶的情况，以一次函数的图象的形式画在了同一直角坐标系中，如图(2)所示。

①由图象、确定甲、乙两车的行驶方向，速度的大小及出发前两车的位置

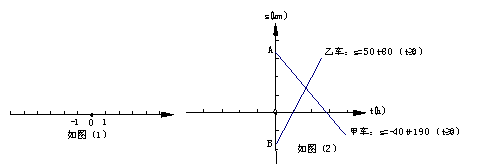②甲、乙两车能否相遇？如能相遇，求相遇时的时刻及在公路上的位置，如不能相遇，请说明理由。

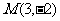23．有两个一次函数，学生甲解出它们图象的交点是，学生乙因把c抄错了而解出它们的图象的交点为。

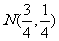(1)求这两个一次函数的解析式

(2)求这两个函数的图象与y轴围成的三角形的面积。

．

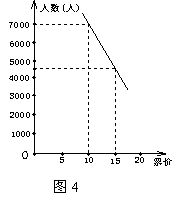
22．某博物馆每周都吸引大量中外游客前来参观．如果游客过多, 对馆中的珍贵文物会产生不利影响．但同时考虑到文物的修缮和保存等费用问题,还要保证一定的门票收入．因此,博物馆采取了涨浮门票价格的方法来控制参观人数． 在该方法实施过程中发现:每周参观人数与票价之间存在着如图4所示的一次函数关系．在这样的情况下,如果确保每周4万元的门票收入,那么每周应限定参观人数是多少?门票价格应是多少元?

21．有一个一次函数的图象，张明，李刚分别说出了它的两个特征．

张明：的解是。

李刚：图象与坐标轴所围成的三角形的面积是9。

你知道这个一次函数的关系式吗？写出你的过程来。

20．生物学家研究表明，某种蛇的长度y (cm)是其尾长x (cm)的一次函数，当蛇的尾长为6cm时，蛇长为45．5cm；当尾长为14cm时，蛇长为105．5cm．当一条蛇的尾长为10cm时，这条蛇的长度是＿＿＿cm．