
=200x+8600.
(2)由W=200x+8600≤9000,得x≤2,
∴x=0,1,2,共有3种调运方案.
(3)当x=0时,总运费最低,即从A市调10台给C村,调2台给D村,从B市调6台给D村,为总运费最低的调运方案,最低运费为8600元.
函数的综合应用题往往综合性强,覆盖面广,包含的数学思想方法多。它能真正考查学生运用所学知识解决实际问题的能力。一次函数的综合应用题常出现于销售、收费、行程等实际问题当中,通常是以图象信息的形式出现。
1、成本与利润问题。
例1:一次时装表演会预算中票价定位每张100元,容纳观众人数不超过2000人,毛利润y(百元)关于观众人数x(百人)之间的函数图象如图所示,当观众人数超过1000人时,表演会组织者需向保险公司交纳定额平安保险费5000元(不列入成本费用)请解答下列问题:⑴求当观众人数不超过1000人时,毛利润y(百元)关于观众人数x(百人)的函数解析式和成本费用s(百元)关于观众人数x(百人)的函数解析式;
⑵若要使这次表演会获得36000元的毛利润,那么要售出多少张门票?需支付成本费用多少元?
(注:当观众人数不超过1000人时,表演会的毛利润=门票收入-成本费用;当观众人数超过1000人时,表演会的毛利润=门票收入-成本费用-平安保险费)
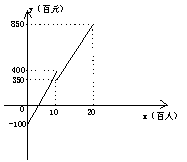
解析:⑴由图象可知:当0≤x≤10时,设y关于x的函数解析y=kx-100,
∵(10,400)在y=kx-100上,∴400=10k-100,解得k=50
∴y=50x-100,s=100x-(50x-100),∴s=50x+100
⑵当10<x≤20时,设y关于x的函数解析式为y=mx+b,
∵(10,350),(20,850)在y=mx+b上,
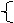
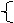 ∴ 10m+b=350 解得 m=50
∴ 10m+b=350 解得 m=50
20m+b=850 b=-150
∴y=50x-150 ∴s=100x-(50x-150)-50∴s=50x+100
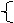 ∴y= 50x-100 (0≤x≤10)
∴y= 50x-100 (0≤x≤10)
50x-150 (10<x≤20) 令y=360 当0≤x≤10时,50x-100=360 解得x=9.2 s=50x+100=50×9.2+100=560 当10<x≤20时,50x-150=360解得x=10.2 s=50x+100=50×10.2+100=610。要使这次表演会获得36000元的毛利润. 要售出920张或1020张门票,相应支付的成本费用分别为56000元或61000元。
点评:此题是借助函数图象确定函数关系式,从而进行经济决策的经济问题。题中需注意提示和分段函数的分情况讨论。
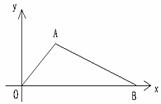
27、观察函数图象,并根据所获得的信息回答问题:
(1)折线OAB表示某个实际问题的函数图象,请你编写一道符合图象意义的应用题;
(2)根据你所给出的应用题,分别指出x轴,y轴所表示的意义,并写出A,B两点的坐标.
(3)求出图象AB的函数解析式,并注明自变量x的取值范围.
26、(8分)电视台为某个广告公司特约播放甲、乙两部连续剧.经调查,播放甲连续剧平均每集有收视观众20万人次,播放乙连续剧平均每集有收视观众15万人次,公司要求电视台每周共播放7集.
(1)设一周内甲连续剧播x集,甲、乙两部连续剧的收视观众的人次的总和为y万人次,求y关于x的函数关系式;
(2)已知电视台每周只能为该公司提供不超过300分钟的播放时间,并且播放甲连续剧每集需50分钟,播放乙连续剧每集需35分钟,请你用所学知识求电视台每周应播放甲、乙两部连续剧各多少集,才能使得每周收看甲、乙连续剧的观众的人次总和最大,并求出这个最大值.
25、(7分)随着我国人口增长速度的减慢,小学入学儿童数量有所减少,下表中的数据近似地呈现了某地区入学儿童人数的变化趋势,试用你所学的函数知识解决下列问题:
(1)求入学儿童人数y(人)与年份x(年)的函数关系式;
(2)利用所求函数关系式,预测该地区从哪一年起入学儿童的人数不超过1000人?
|
年份(x) |
2000 |
2001 |
2002 |
… |
|
入学儿童人数(y) |
2520 |
2330 |
2140 |
… |
24、(6分)某地电话拨号入网有两种收费方式,用户可以任选其一:
A、 计时制:0.05元/分;
B、 包月制:50元/月(限一部个人住宅电话上网)
此外,每一种上网方式都得加收通信费0.02元/分.
(1) 请你分别写出两种收费方式下用户每月应支付的费用y(元)与上网时间x(小时)之间的函数关系式;
(2) 若某用户估计一个月上网的时间为20小时,你认为采用哪种方式较为合算?
23、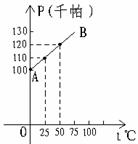 (6分) 科学家通过实验探究出一定质量的某气体在体积不
(6分) 科学家通过实验探究出一定质量的某气体在体积不
变的情况下,压强P(千帕)随温度t(℃)变化的函数关系式
是P=kt+b,其图像是如图所示的射线AB,请根据图像求出上
述气体的压强P与温度t的函数关系式.
22、(6分)小强在劳动技术课中要制作一个周长为80cm的等腰三角形,请你写出底边长y(cm)与一腰长x(cm)的函数关系式和自变量x的取值范围.
21、(5分)下表是小磊往姥姥家打长途电话的几次收费记录.
|
时间(min) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
电话费 (元) |
0.3 |
0.6 |
0.9 |
1.2 |
1.5 |
1.8 |
2.1 |
(1) 上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2) 如果用x(min)表示时间,用y(元)表示电话费,那么随着x的变化,y的变化趋势是怎样的?
20、如图,直线y=-2x+10与x轴、y轴分别交于A、B
两点,把△AOB沿AB翻折,点O落在C处,则C点的坐标
为 .
19、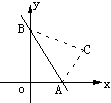 一次函数y=kx+3的图象经过点A(2,5),且B(3,a)
一次函数y=kx+3的图象经过点A(2,5),且B(3,a)
和C(b,0)两点在该函数的图象上,则a-b= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com