
7.若直线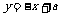 和直线
和直线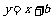 的交点坐标为(
的交点坐标为(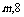 ),则
),则 ____________.
____________.
6.出租车收费按路程计算,3km内(包括3km)收费8元;超过3km每增加1km加收1元,则路程x≥3km时,车费y(元)与x (km)之间的函数关系式是________________.
5.将直线y=3x向下平移5个单位,得到直线 ;将直线y=-x-5向上平移5个单位,得到直线 .
4.一次函数的图象经过点(-2,3)与(1 ,-1),它的解析式是___ _____.
3.函数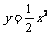 中,当x=___________时,函数的值等于2.
中,当x=___________时,函数的值等于2.
2.在函数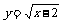 中,自变量
中,自变量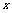 的取值范围是_________.
的取值范围是_________.
1.在球的体积公式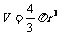 中,变量是________,常量是_________.
中,变量是________,常量是_________.
8.2÷0.25=32.8 ∴课间10分钟内最多有32个同学能及时接完水。
点评:这是2005年泰州市的一道中考题,主要考查的是学生对图象的识读能力,能否围绕图象来解决问题。在考试中有相当一部分同学把问题简单化了,片面认为两个放水管的工作效率是单独一个放水管工作时效率的2倍。这样一来,得出:每个同学接水需0.5分钟,22个同学接水需:(22-4)÷2×0.5+2=6.5(分钟)。从图象上不难得出:两个放水管的工作效率= ,单独一个放水管工作时效率=
,单独一个放水管工作时效率=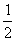 ,
,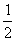 ×2≠
×2≠ 。
。
3、饮水问题。
例3:教室里放有一台饮水机,饮水机上有两个放水管。课间同学们到饮水机前用茶杯接水。假设接水过程中水不发生泼洒,每个学声所接的水量是相等的。两个放水管同时打开时,它们的流量相同。放水时先打开一个水管,过一会再打开第二个水管,放水过程中阀门一直开着。饮水机的存水量y(升)与放水时间x(分钟)的函数关系如下图所示:

⑴求出饮水机的存水量y(升)与放水时间x(分钟)(x≥2)的函数关系式;
⑵如果打开第一个水管后,2分钟时恰好有4个同学接水接束,则前22个同学接水结束共需要几分钟?
⑶按⑵的放法,求出在课间10分钟内最多有多少个同学能及时接完水?
解析:⑴设存水量y与放水时间x的函数解析式为y=kx+b,
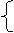 把(2,17)、(12,8)代入y=kx+b,得 17=2k+b 解得 k=-
把(2,17)、(12,8)代入y=kx+b,得 17=2k+b 解得 k=- b =
b =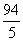
8=12k+b
∴y=- x+
x+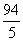 (2≤x≤
(2≤x≤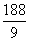 )
)
⑵由图象可得每个同学接水量为0.25升,则前22个同学需接水0.25×22=5.5(升),存水量y=18-5.5=12.5(升)∴12.5=- x+
x+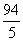 解得 x=7
解得 x=7
∴前22个同学接水共需要7分钟。
⑶当x=10时,存水量y=- ×10+
×10+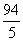 =
=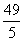 ,用去水18-
,用去水18-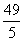 =8.2(升)
=8.2(升)
2、行程问题。
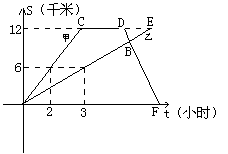
例2:甲乙两名同学进行登山比赛,图中表示甲乙沿相同的路线同时从山脚出发到达山顶过程中,个自行进的路程随时间变化的图象,根据图象中的有关数据回答下列问题:
⑴分别求出表示甲、乙两同学登山过程中路程s(千米)与时间t(时)的函数解析式;(不要求写出自变量的取值范围)
⑵当甲到达山顶时,乙行进到山路上的某点A处,求A点距山顶的距离;
⑶在⑵的条件下,设乙同学从A点继续登山,甲同学到达山顶后休息1小时,沿原路下山,在点B处与乙同学相遇,此时点B与山顶距离为1.5千米,相遇后甲、乙各自沿原路下山和上山,求乙到大山顶时,甲离山脚的距离是多少千米?
解析:⑴设甲、乙两同学登山过程中,路程s(千米)与时间t(时)的函数解析式分别为s =k
=k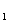 t,s
t,s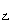 =k
=k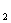 t。
t。
由题意得:6=2 k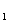 ,6=3 k
,6=3 k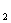 ,解得:k
,解得:k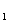 =3,k
=3,k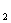 =2 ∴s
=2 ∴s =3t,s
=3t,s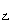 =2t
=2t
⑵当甲到达山顶时,s =12(千米),∴12=3t 解得:t=4∴s
=12(千米),∴12=3t 解得:t=4∴s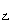 =2t=8(千米)
=2t=8(千米)
⑶由图象可知:甲到达山顶宾并休息1小时后点D的坐标为(5,12)
由题意得:点B的纵坐标为12-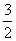 =
=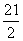 ,代入s
,代入s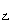 =2t,解得:t=
=2t,解得:t=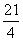
∴点B(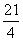 ,
,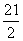 )。设过B、D两点的直线解析式为s=kx+b,由题意得
)。设过B、D两点的直线解析式为s=kx+b,由题意得
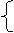
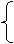
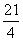 t+b=
t+b=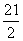 解得:
k=-6
解得:
k=-6
5t+b=12 b=42
∴直线BD的解析式为s=-6t+42 ∴当乙到达山顶时,s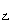 =12,得t=6,把t=6代入s=-6t+42得s=6(千米)
=12,得t=6,把t=6代入s=-6t+42得s=6(千米)
点评:借助函数图象表达题目中的信息,读懂图象是关键。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com