
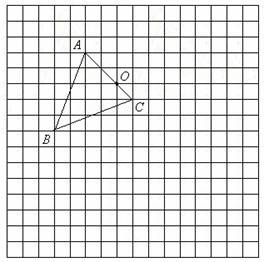
2.下图中,先画出△ABC绕着点O逆时针旋转135º后的△A′B′C′,再画出△A′B′C′向下平移3个单位后的△A′′B′′C′′。
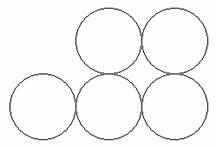
1.如图所示的两个三角形成中心对称,画出它们的对称中心。
归纳小结:在应用轴对称、平移、旋转三种变换解有关推理题目时,应牢牢把握住变换后图形的形状和大小都没有改变,线段的长度和角的大小都不变,前后两个图形能完全重合。
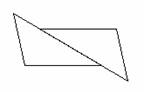
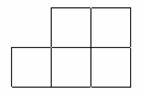
3.下图有5个相同的正方形组成,试用一条直线将它分成面积相等的两部分。
2.如图,已知△ABC中,点D为BC的中点:
(1)画出以点D为对称中心,且与△ADC对称的△EDB;
(2)BE和AC有什么关系?为什么?
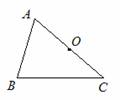
1.已知△ABC和点O,画出△ABC关于点O对称的三角形。

3.课堂练习:
2.例题:[实践应用]教法说明:以下例题采取学生先练习,然后教师讲评,也可以采取师生共同完成的方法进行教学。
例1:按下列要求画出正确图形:
(1)已知△ABC和线段PQ,画出△ABC沿线段PQ的方向平移3cm后的图形;
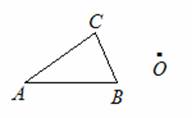
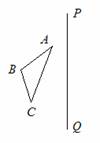

(2)已知△ABC和直线PQ,画出△ABC关于直线PQ对称的三角形;
(3)已知△ABC和点O,画出△ABC关于点O对称的三角形。
 解:如下图所示:
解:如下图所示:
 (1)
(2) (3)
(1)
(2) (3)
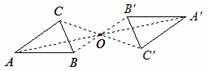
例2:按要求画出对称轴或对称中心:
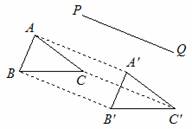
(1)已知△ABC和△A′B′C′关于某条直线成轴对称,画出它们的对称轴;
(2)已知△ABC和△A′B′C′关于某一点成中心对称,画出对称中心。
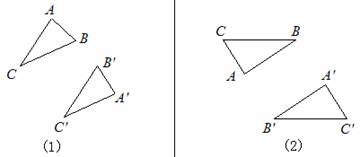
解:如下图所示:(1)直线PQ就是所求的对称轴。(2)点O就是所求的对称中心。

例3:下形中既是中心对称图形,又是轴对称图形的是( )。
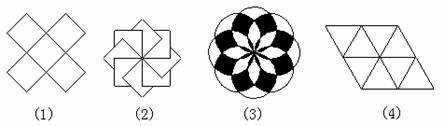
解:图中(1)、(3)、(4)都符合条件。
例4:如图,正方形ABCD的BC边上一点E,将△ABE绕点B逆时针旋转90º,再沿着BC方向平移,平移距离是线段BC的长度,此时三角形的斜边与AE有什么关系?请画出图形。
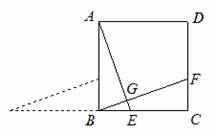
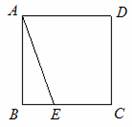
解:如图所示,此时三角形的斜边BF与AE相等并且垂直。
因为△ABE经过旋转、平移后到达△BCF的位置。所以△ABE和△BCF是互相重合的。
所以BF=AE,∠BAE=∠CBF。因为∠BAE+∠BEA=90º,所以∠CBF+∠BEA=90º,所以∠BGE=90º。所以BF⊥AE。
1.探究归纳:
根据知识结构复习相关的知识要点,并回答以下问题:
(1)什么是图形的平移?平移的特征是什么?
(2)什么是图形的旋转?旋转的特征是什么?
(3)什么是旋转对称图形?它和中心对称图形有什么区别?
(4)什么是中心对称图形?什么叫两个图形成中心对称?
(5)如果两个图形成中心对称图形,那么它们有什么特征?
(6)两个图形成中心对称的识别方法是什么?
(7)图形的三种主要变换:平移、旋转、轴对称有什么共同的特征?
评:其中第7小题的答案是:在这些变换过程中,图形的形状和大小都没有改变,线段的长度和角的大小都不变。
这是图形变换最主要的特征,是将来进一步研究图形全等及其有关性质的基础。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com