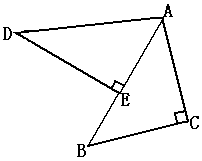
4．△ABC与△ADE都是等腰直角三角形，∠C和∠AED都是直角，点E在AB上，△ADE经过旋转后能与△ABC重合，请回答下列问题

(1)哪一点是旋转中心？

(2)旋转了多少度？

(3)线段AD与AC相等吗？为什么？

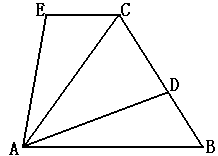
3．△ABC是等边三角形，D是BC上一点，△ABD经旋转后到达△ACE的位置。

(1)旋转中心是哪一点

(2)旋转了多少度？

(3)若M是AB的中点，那么经过上述旋转后，点M转到了什么位置？

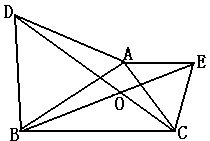
2．等边△ABD和等边△ACE，∠BAC=90°，BE与CD交于O，△ACD绕点A旋转多少度后能与△AEB重合？CD与BE有何关系？

例1．△ABE中，AB=4cm，AE=3cm，∠A=20°，将△ABE沿着MN方向,平移2cm。到△FCD的位置，则①BC、CF的长是多少？②∠CFD的度数能求吗？若能求，请你求出来。

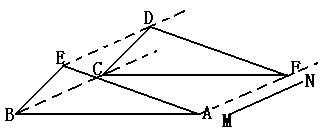
解：①点B移动2cm到点C，则BC=2cm，线段CF与BA是对应线段，即CF=BA=4cm

②∠CFD与∠A是对应角，即∠CFD=∠A=20°。

例2．如图，正方形ABCD，E是CD上一点，△ADE经过旋转后到达△ABF的位置。

①旋转中心是哪一点？

②旋转角度是多少度？

③旋转后的线段与原线段的位置有何关系？

④如果M是AE的中点，那么经过上述旋转后，点M转到了什么位置？

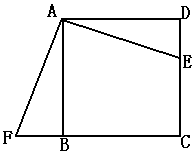
解：①旋转中心是A点

②旋转角度是90度

③旋转后的线段与原线段垂直

④如果M是AE的中点，那么经过上述旋转后，点M转到了AF的中点

例3．如图，AB与CD交于O，且∠AOC=60°，AB=CD=1，求证：AC+BD≥1

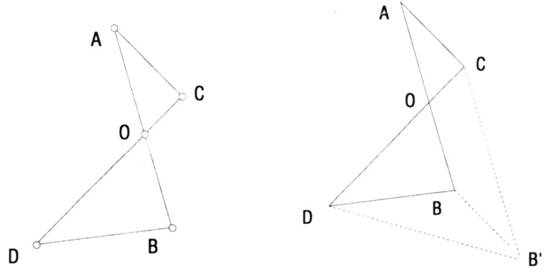
分析：考虑到应将AC、BD和AB移到同一个三角形中，采用平移交换

解：将AB沿着AC方向平移线段AC的长度到CB＇，连接DB＇、BB＇。

如图，则AC= BB＇，CB＇平行且等于AB，且由AB=CD=1，可得CB＇=CD；又∠AOC=60°，得∠DCB′=60°，所以△CDB＇是等边三角形，即DB＇=1，在三角形DBB＇中，DB+BB＇> DB＇，即AC+BD>1。

当D，B，B＇三点共线时，AC+BD=1

综上所述，AC+BD≥1

例4．△ABC是等边三角形，它绕哪一点旋转多少度后能与自身重合？

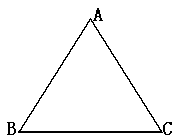
分析：不妨设旋转某个角度后C与A重合，A与B重合，B与C重合。由于旋转中心到两个对应点的距离相等，设旋转中心为O，即OA=OC，OB=OC，则O点一定是△ABC的边AC、BC的垂直平分线的交点，又△ABC是等边三角形，则O点也是△ABC的中线(高线、角平分线)的交点。

解：设等边△ABC的中线的交点为O，则△ABC绕点O旋转120°后能与自身重合。

我们把旋转某个角度后能与自身重合的图形叫做旋转对称图形。

例5．园林小路，曲径通幽。如图所示的小路由白色正方形石板和青、红两色的三角形石板铺成。问：内圈三角形石板的总面积大，还是外圈三角形石板的总面积大？请说明理由。

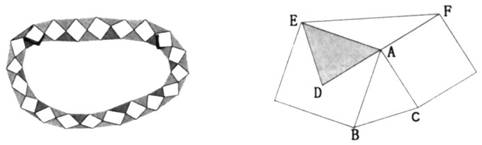
分析：请同学们仔细观察图形的结构：容易看出，两个相邻的正方形只有一个顶点重合，它们之间夹着一个外圈的三角形石板与一个内圈的三角形石板。因此内、外圈三角形总个数是相等的。

我们取两个相邻的正方形石板与所夹的内外圈各一个三角形石板的构图分析，如图，不难发现∠EAF+∠BAC=180°。将△BAC绕A点顺时针旋转90°补到△EAD的位置。由于∠EAF+∠BAC=180°，所以D、A、F在一条直线上。又AD=AC，从而AD=AF。于是△EAD与△EAF是等底同高的三角形，因此它们的面积相等。也就是△ABC与△EAF的面积相等。由于两个相接触的正方形所夹的外圈三角形面积等于内圈三角形面积，所以内圈三角形石板总面积等于外圈三角形石板的总面积。

解：将△ABC绕A点顺时针旋转90°到△AED的位置。则由旋转的特征知道AD=AC，∠BAC=∠EAD。又由正方形的性质可知AF=AC，即得AD=AF，又由∠EAF+∠BAC=180°，可知∠EAD+∠EAF=180°，即D、A、F三点在同一条直线上，此时△EDA与△EAF的面积相等。又由于内、外圈三角形石板的个数相等，则内圈三角形石板与外圈三角形石板的总面积相等。

[同步达纲练习]

1．将下图沿着MN的方向平移2cm

2．旋转特征

(1)旋转后的图形与原图形的形状和大小都没有发生变化。

(2)旋转后的对应线段相等。

(3)旋转后的对应角相等。

(4)旋转后对应点到旋转中心的距离相等。

1．△ABC绕着点O旋转60°后得到△DEF，我们可以看到点A旋转到点D，线段BA旋转到ED，∠BAC旋转到∠EDF，这些都是互相对应的点，线段和角，图形的旋转由旋转中心和旋转的角度所决定。其中，线段AC的对应线段是DF，∠B的对应角是∠E，O点叫做旋转中心，它是旋转中唯一不动的点。

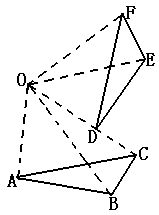
由于图形中的每一点都绕着旋转中心旋转了同样大小的角度，因此我们可以得到旋转的特征如下：

3．平移特征

(1)平移后的图形与原图形的形状和大小都没有发生变化。

(2)平移后的对应线段平行且相等(在平移过程中，对应线段也可能在同一条直线上)。

(3)平移后的对应角相等。

(4)平移后对应点所连的线段平行且相等。

2．再请同学们回忆一下用直尺与三角板画平行线的方法。

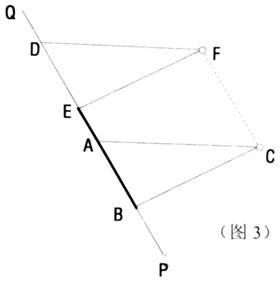
如图3，将△ABC沿着直尺PQ平移到△DEF，就可以画出AC的平行线DF了。

△ABC平移的方向是由点B到点E的方向，平移的距离就是线段BE的长度。

因此平移后对应点所连的线段平行且相等。

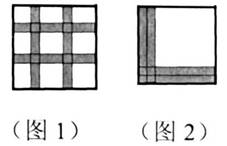
1．现有一条白色的正方形手帕，它的边长是18厘米，手帕上横竖各有二道红条，如图1中阴影所示部分，红条宽都是2厘米。问这条手帕白色部分的面积是多少？

分析与解答：

由于手帕的边长是18厘米，所以正方形手帕的面积是324平方厘米，要求白色部分的面积，只需减去红色部分的面积就可以了。

红色部分是四个长为18厘米宽为2厘米的红色长条，这四个红色长条的面积是4×18×2=144平方厘米。但每个横红条与竖红条在交叉口处又重叠一个边长为2厘米的正方形，即多算了4平方厘米，因此两个横红条与两个竖红条共重叠16平方厘米，所以红条覆盖的面积是144-16=128平方厘米。这条手帕白色部分的面积是324-128=196平方厘米。

你有更好的计算方法吗？小明同学是这样想的：把竖的两个红条位置平行移动一下，使它们恰好紧贴在一起，再移到正方形的最左端的边上，把横的两块红条也做类似的平移，使它们和正方形的最底下的边紧贴，如图2。这样平移横、竖红条后所得图形的白色部分面积不变，而此时白色部分的面积一目了然，它等于边长为14厘米的正方形的面积，即196平方厘米。

这种图形的平行移动简称平移，由移动的方向和距离所决定。

大楼电梯上上下下地迎送来客；火车在笔直的铁轨上飞驰而过；飞机在起飞前加速滑行等，这些都给我们带来物体平行移动的形象。

4、中心对称与轴对称等等的作图与应用要注意图形的相对性与图形的关系。