
9.下列说法:①若a≠0,m,n是任意整数,则am.an=am+n; ②若a是有理数,m,n是整数,且mn>0,则(am)n=amn ;③若a≠b且ab≠0,则(a+b)0=1;④若a是自然数,则a-3.a2=a-1.其中,正确的是( ).
(A)① (B)①② (C)②③④ (D)①②③④
8.汽车从甲地开往乙地,每小时行驶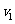 km,t小时可以到达,如果每小时多行驶
km,t小时可以到达,如果每小时多行驶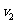 km,那么可以提前到达的小时数为 ( )
km,那么可以提前到达的小时数为 ( )
(A)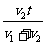 (B)
(B) 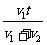 (C)
(C)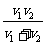 (D)
(D)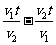
7.一水池有甲乙两个进水管,若单独开甲、乙管各需要a小时、b小时可注满空池;现两管同时打开,那么注满空池的时间是( )
(A)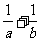 (B)
(B)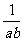 (C)
(C) (D)
(D)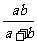
6.若分式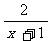 的值为正整数,则整数x的值为( )
的值为正整数,则整数x的值为( )
(A)0 (B)1 (C)0或1 (D)0或-1
5.分式方程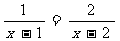 ( ).
( ).
(A)无解 (B)有解x=1 (C)有解x=2 (D)有解x=0
4.计算 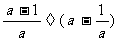 的正确结果是( ).
的正确结果是( ).
(A)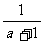 (B)1
(C)
(B)1
(C)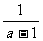 (D)-1
(D)-1
3.化简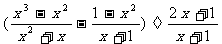 的结果为( ).
的结果为( ).
(A)x-1 (B)2x-1 (C)2x+1 (D)x+1
2.化简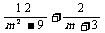 的结果是( ).
的结果是( ).
(A) (B)
(B)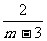 (C)
(C) (D)
(D)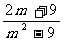
1.已知x≠y,下列各式与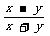 相等的是( ).
相等的是( ).
(A)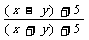 (B)
(B)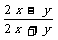 (C)
(C) 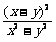 (D)
(D)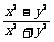
16. 某商场在一楼与二楼之间装有一部自动扶梯,以均匀的速度向上行驶,一男孩与一女孩同时从自动扶梯上走到二楼(扶梯本身也在行驶).如果二人都做匀速运动,且男孩每分钟走动的级数是女孩的两倍.又已知男孩走了27级到达顶部,女孩走了18级到达顶部(二人每步都只跨1级).
(1)扶梯在外面的部分有多少级.
(2)如果扶梯附近有一从二楼下到一楼的楼梯,台阶级数与扶梯级数相等,这两人各自到扶梯顶部后按原速度走下楼梯,到一楼后再乘坐扶梯(不考虑扶梯与楼梯间的距离).则男孩第一次追上女孩时,他走了多少台阶?
解: (1)设女孩速度为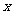 级/分,电梯速度为
级/分,电梯速度为 级/分,楼梯(扶梯)为
级/分,楼梯(扶梯)为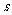 级,则男孩速度为
级,则男孩速度为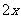 级/分,依题意有
级/分,依题意有
 ①
①
把方程组①中的两式相除,得 ,解得
,解得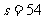 .
.
因此楼梯有54级.
(2)设男孩第一次追上女孩时,走过扶梯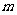 次,走过楼梯
次,走过楼梯 次,则这时女孩走过扶梯
次,则这时女孩走过扶梯 次,走过楼梯
次,走过楼梯 次.
次.
将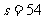 代入方程组①,得
代入方程组①,得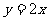 ,即男孩乘扶梯上楼的速度为
,即男孩乘扶梯上楼的速度为 级/分,女孩乘扶梯上楼的速度为
级/分,女孩乘扶梯上楼的速度为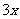 级/分.于是有
级/分.于是有
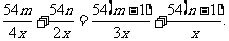
从而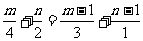 ,即
,即 .
.
无论男孩第一次追上女孩是在扶梯上还是在下楼时, 中必有一个为正整数,且
中必有一个为正整数,且 ,经试验知只有
,经试验知只有 符合要求.
符合要求.
这时,男孩第一次追上女孩所走过的级数是: (级).
(级).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com