2、正方形具有而矩形不一定具有的性质是(　)

A、对角线互相平分　　　　　　　 B、对角线相等

C、四个角都相等　　　　　　　　 D、对角线互相垂直

1、下列图形中哪个既是轴对称图形，又是中心对称图形？(　)

A、等边三角形　　　　　　　　　 B、平行四边形

C、菱形　　　　　　　　　　　　 D、等腰梯形

3、等腰梯形需要应用好腰与底角的特殊性质。

2、梯形的应用主要是辅助线的作法与应用；

1、平行四边形的性质与判定主要要看清题设与结论，不能把性质与判定混

　　用；

例题1:如图所示，在□ABCD中，E、F分别是边AD、BC的中点，则EB与DF间存

　　　在什么关系？

分析与解：EB平行且等于DF。

思考：若AE=1/3·AD，CF=1/3·BC，则EB与DF的关系仍成立吗？为什么？

　　　AE=1/n·AD，CF=1/n·BC呢？若E、F分别是AD、CB延长线上的点，且

　　　 DE=BF，则EB与DF的关系仍成立吗？为什么？

例题2：如图，在△ABC中AB=AC，点P是BC的三等分点，过P作PE∥AC，PF∥

　　　 AB，分别交AB、AC于E、F，试说明四边形AEPF的周长是线段AB的两

　　　 倍。

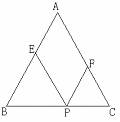
分析与解： 因为AB=AC　　 所以∠B=∠C。又因为PE∥AC　 所以∠C=∠EPB=∠B

　　　　　　　　　　　 可知PE=EB　　 又因为PE∥AC，PF∥AB

　　　　　　 所以　　 四边形AEPF是平行四边形　 可知　 PF=AE，AF=PE

　　　　　　　　　　　　因此　 四边形AEPF的周长=2PE+2AE=2EB+2AE=2AB

思考：随着点P的移动(在BC上)，上述结论是否改变？能说明理由吗？

例题3:如图，为一平行四边形，请你用不同的方法将平行四边形的面积四等分。

　　　 (至少三种以上)

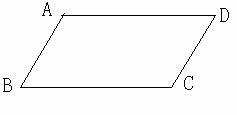
分析与解：(作图略)

思考：还有其它的分法吗？你共能想出多少种不同的分法？动手试试吧。

例题4: 如图，△ABC中，BD平分∠ABC，DE∥BC，EF∥AC，试确定CF与BE的

　　　　大小关系，并说明关系的正确性。

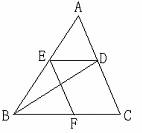
分析与解：CF与BF的关系为相等。理由：由角平分线及DE∥BC得BE=DE，由

　　　　　CDEF为平行四边形可知DE=CF，故BE=CF

思考：若AB=AC，则EB=EF=DC=ED=FC，你知道其中的奥秘吗？

例题5：如图，在直角梯形ABCD中，DC∥AB，DA⊥AB于A，AE⊥BC于E，且

　　　 AB=BC，试说明CD=CE。

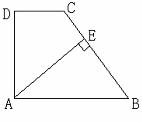
分析与解：连AC，易证∠DCA=∠BCA，由角平分线性质定理可知：CD=CE。

思考：角平分线有何性质？本题除了用角平分线性质来说明外，还可用其它方法

　　　吗？(提示：过C作CF⊥AB于F，用等腰三角形的有关性质来说明)

12、等腰梯形同一底上　 两个内角　 相等，两条对角线　 相等　　 ；

11、　　　　 两腰相等　　　 的梯形叫做等腰梯形，有一个角是　 直角　 的

　　　梯形叫做直角梯形；

10、只有　　 一组对边平行　　 的四边形叫做梯形；

9、两组对边　　　　 分别平行　　　　 的四边形是平行四边形；