5．练习：填空：

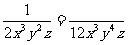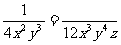(1)；　 (2)；　 (3)。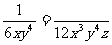

求下列各组分式的最简公分母：

(1)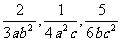；　　　　 (2)；

　　　 (3)

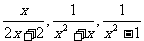
4．所得的系数的最小公倍数与各字母(或因式)的最高次幂的积(其中系数都取正数)即为最简公分母。

3．相同字母(或因式)的幂取指数最大的；

2．各分式的分母中所有字母或因式都要取到；

4．讨论：　 (1)求分式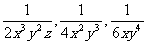的(最简)公分母。

分析：对于三个分式的分母中的系数2，4，6，取其最小公倍数12；对于三个分式的分母的字母，字母x为底的幂的因式，取其最高次幂x³，字母y为底的幂的因式，取其最高次幂y⁴，再取字母z。所以三个分式的公分母为12x³y⁴z。

(2) 求分式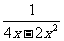与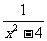的最简公分母。

分析：先把这两个分式的分母中的多项式分解因式，即

　　　　　　　　 4x-2x²= -2x(x-2)，x²-4=(x+2)(x-2)，

把这两个分式的分母中所有的因式都取到，其中，系数取正数，取它们的积，即2x(x+2)(x-2)就是这两个分式的最简公分母。

请同学概括求几个分式的最简公分母的步骤。

答：1．取各分式的分母中系数最小公倍数；

3．和分数通分类似，把几个异分母的分式化成与原来的分式相等的同分母的分式叫做分式的通分。

通分的关键是确定几个分式的公分母。

2．什么叫分数的通分？

　　 答：把几个异分母的分数化成同分母的分数，而不改变分数的值，叫做分数的通分。

1．把分数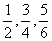通分。

解　 ，，。

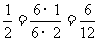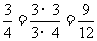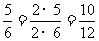例1　 不改变分式的值，使下列分式的分子和分母都不含“-”号：

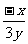(1)；　　　 (2)；　　　 (3).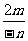

例2　 不改变分式的值，使下列分式的分子与分母的最高次项的系数是正数：

(1)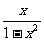；　　　　　 (2).

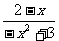注意：(1)根据分式的意义，分数线代表除号，又起括号的作用。

(2)当括号前添“+”号，括号内各项的符号不变；当括号前添“-”号，括号内各项都变号。

例3若x、y的值均扩大为原来的2倍，则分式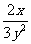的值如何变化？若x、y的值均变为原来的一半呢？

2．分式的基本性质。