
2、概 括
上述解分式方程的过程,实质上是将方程的两边乘以同一个整式,约去分母,把分式方程转化为整式方程来解.所乘的整式通常取方程中出现的各分式的最简公分母.
1、思 考 : 怎样解分式方程呢?
为了解决本问题,请同学们先思考并回答以下问题:
1)、回顾一下一元一次方程时是怎么去分母的,从中能否得到一点启发?
2)有没有办法可以去掉分式方程的分母把它转化为整式方程呢?
试动手解一解方程(1).
方程(1)可以解答如下:
方程两边同乘以(x+3)(x-3),约去分母,得
80(x-3)=60(x+3).
解这个整式方程,得
x=21.
所以轮船在静水中的速度为21千米/时.
4、辨析:判断下列各式哪个是分式方程.
(1)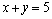 ; (2)
; (2)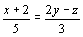 ; (3)
; (3)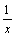 ; (4)
; (4)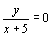 ; (5)
; (5)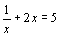
根据定义可得:(1)、(2)是整式方程,(3)是分式,(4)(5)是分式方程.
3、概 括
方程(1)有何特点?
让学生观察分析后,发表意见,达成共识:
方程(1)中含有分式,并且分母中含有未知数,像这样的方程叫做分式方程.
教师提问:你还能举出一个分式方程的例子吗?
让学生举出分式方程的例子,根据分式方程的概念进行判定,加深对分式方程概念的理解。
2、分析:
设轮船在静水中的速度为x千米/时,根据题意,得
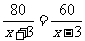 . (1)
. (1)
1、问题:轮船在顺水中航行80千米所需的时间和逆水航行60千米所需的时间相同.
已知水流的速度是3千米/时,求轮船在静水中的速度.
2.使学生激发学习数学的兴趣,同时提高解决问题的信心.
过程性目标
重点:列分式方程解实际问题;
难点:列分式方程解实际问题中的方程根的检验.
教学过程
|
师生活动 |
备注 |
|
一、创设情境 例1 某校招生录取时,为了防止数据输入出错,2640名学生的成绩数据分别由两位程序操作员各向计算机输入一遍,然后让计算机比较两输入是否一致.已知甲的输入速度是乙的2倍,结果甲比乙少用了2小时输完,问这两个操作员每分钟各能输入多少名学生的成绩? 思考 (1)问题中的等量关系是什么? (2)为列出等量关系应怎样设定未知数? 分析 (1)设乙每分钟能输入x名学生的成绩,则甲每分钟能输入2x名学生的成绩. (2)甲输入所花的时间是 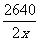 分钟,乙输入所花的时间是 分钟,乙输入所花的时间是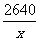 分钟. 分钟.二、探究归纳 讨论、总结 解决类似于上述问题应有以下步骤: (1)分析题意; (2)设出适当的未知数; (3)分析题中的相等关系,列出相关的代数式,列出方程; (4)解方程,并检验; (5)写出答案. 注 这里的检验分两层意思: (1)检验解出的根是否是原方程的根; (2)原方程的根是否符合实际情况. 三、实践应用 (例1)解 设乙每分钟能输入x名学生的成绩,则甲每分钟能输入2x名学生的成绩,根据题意得 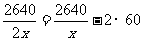 .解得x=11. .解得x=11.经检验,x=11是原方程的解.并且x=11时,2 x=2×11=22,符合题意. 答 甲每分钟能输入22名学生的成绩,乙每分钟能输入11名学生的成绩. 例2 已知A、B两地相距36千米,甲、乙两人分别从A、B两地同时出发,相向而行,相遇时,甲距B地还有16千米,相遇后,继续前进,甲到B地比乙到A地早1.8小时,求甲、乙两人速度. 分析 (1)解决此类问题通过画线段图能帮助对题意的理解; 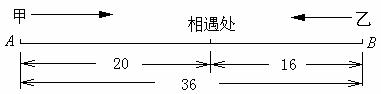 (2)相遇时,甲距B地还有16千米,说明甲此时走了(36-16)千米,即20千米,乙走了16千米,从出发到相遇,两人所用时间相等; (3)设甲的速度为x千米/时,则乙的速度为  千米/时; 千米/时;(4)走完全程甲用了 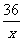 小时,乙用了 小时,乙用了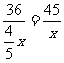 小时. 小时.解 设甲的速度为x千米/时,则乙的速度为  千米/时, 千米/时,根据题意,得 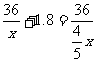 . .解这个方程,得 x=5. 经检验,x=5是原方程的根, 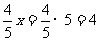 ,符合题意. ,符合题意.答 甲的速度为5千米/时,则乙的速度为4千米/时. 四、交流反思 1.用分式方程来解决实际问题与前面学过的用一元一次方程解决实际问题的思考分析过程类似; 2.不同的是未知数会出现在分母上(所设方程是分式方程); 3.检验时应分两个方面来思考; 4.针对具体问题要细致分析其中的基本量之间的关系. 五、检测反馈 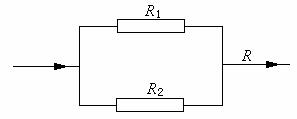 1.电视机、摄像机等电器的电路中有许许多多元件,它们都具有电阻.如图所示,当两个电阻R1、R2并联时,总电阻R满足 1.电视机、摄像机等电器的电路中有许许多多元件,它们都具有电阻.如图所示,当两个电阻R1、R2并联时,总电阻R满足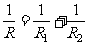 .若R1=10欧,R2=15欧,求总电阻R. .若R1=10欧,R2=15欧,求总电阻R.2.供电局的电力维修工要到30千米远的郊区进行电力抢修.技术工人骑摩托车先走,15分钟后,抢修车装载着所需材料出发,结果他们同时到达.已知抢修车的速度是摩托车的1.5倍,求这两种车的速度. 3.某大商场家电部送货人员与销售人员之比为1:8,今年夏天由于家电购买量明显增多,家电部经理从销售人员中抽调了22人去送货.结果送货人员与销售人员人数之比为2:5.求这个商场家电部原来各有多少名送货人员和销售人员? |
|
1.培养学生分析问题、解决问题的能力和逻辑思维能力;
2.体会数学建模的过程.
情感态度目标
1.让学生对实际问题的分析,学会运用适当的数学工具,体会数学能解决实际问题的广泛用途;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com