1、问题1　　 在§21.1中介绍同底数幂的除法公式a^m÷aⁿ=a^m-n时，有一个附加条件：m＞n，即被除数的指数大于除数的指数.当被除数的指数不大于除数的指数，即m=n或m＜n时，情况怎样呢？

3、解分式方程为什么要进行验根？怎样进行验根？

[布置作业]：

课本第16页练习3、习题1

2、　　　　　　　 解分式方程的一般步骤：

a.　　 在方程的两边都乘以最简公分母，约去分母，化为整式方程．

b.　　 解这个整式方程．

c.验根，即把整式方程的根代入最简公分母，看结果是不是零，若结果不是0，说明此根是原方程的根；若结果是0，说明此根是原方程的增根，必须舍去．

1、　　　　　　　 什么是分式方程？举例说明

8、练习：课本第页练习1、2

[本课小结]：

7、有了上面的经验，我们再来完整地解二个分式方程.

例2　解方程：(1)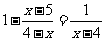　　　　　　　　 (2)　　　　　

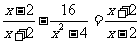
　解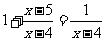： 　　　　　　　　　　　　解：方程两边同乘以 ，得

方程两边同乘以 ，　　　　　　　　　　　　　　　　 　，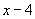

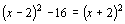得　 ．　　　　　　　　　　　　　　　　　 　，

∴ 　　　　　　　　　　　　　　　　　　　　　　　　　　∴ ．

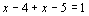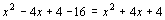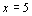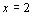检验：把x=5代入 x-5，得x-5≠0　　　　　　　　 检验：把x=2代入 x²-4，得x²-4=0。

所以，x=5是原方程的解.　　　　　　　　　　　　 所以，x=2是增根，从而原方程无解。.　

6、验根的方法

解分式方程进行检验的关键是看所求得的整式方程的根是否使原分式方程中的分式的分母为零.有时为了简便起见，也可将它代入所乘的整式(即最简公分母)，看它的值是否为零.如果为零，即为增根.

如例1中的x=1，代入x²－1＝0，可知x=1是原分式方程的增根.

5．那么，可能产生“增根”的原因在哪里呢？

对于原分式方程的解来说，必须要求使方程中各分式的分母的值均不为零，但变形后得到的整式方程则没有这个要求.如果所得整式方程的某个根，使原分式方程中至少有一个分式的分母的值为零，也就是说使变形时所乘的整式(各分式的最简公分母)的值为零，它就不适合原方程，即是原分式方程的增根.

4、在将分式方程变形为整式方程时，方程两边同乘以一个含未知数的整式，并约去了分母，有时可能产生不适合原分式方程的解(或根)，这种根通常称为增根.

因此，在解分式方程时必须进行检验.

3、例1　解方程：.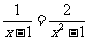

解　方程两边同乘以(x²-1),约去分母，得

x+1=2.

解这个整式方程，得

x=1.

事实上，当x=1时，原分式方程左边和右边的分母(x－1)与(x²－1)都是0，方程中出现的两个分式都没有意义，因此，x=1不是原分式方程的根，应当舍去.所以原分式方程无解.