
(2)若点(-a,y1),(-2a,y2)在反比例函数的图象上,试比较y1与y2的大小;
(3)求△AOB的面积。
答案:
一、
1~5题 B C C B C
6~10题 D A B C C
二、
11.  12.
12. 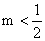 13.
13.  14. 1
15.
14. 1
15.  16.
16.  17. k<-1 18.
17. k<-1 18.
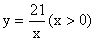 三、
19.
三、
19.  20. (1)a=1 (2)y=x+2
20. (1)a=1 (2)y=x+2
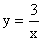 21.
(1)n=2 y=2x-2 (2)(3)略
四、 22.
21.
(1)n=2 y=2x-2 (2)(3)略
四、 22. 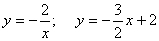
23. (1)A(-1,0) B(0,1) D(1,0) (2)y=x+1  五、
(1)
五、
(1) 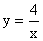 (2)y1<y2
(3)S△AOB=3
(2)y1<y2
(3)S△AOB=3
23.(10分)如图3,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴交于A,B两点,且与反比例函数  的图象的一支在第一象限交于点C,CD垂直于x轴,垂
的图象的一支在第一象限交于点C,CD垂直于x轴,垂 足为D,若OA=OB=OD=1
(1)写出点A,B,D的坐标; (2)求一次函数和反比例函数的解析式;
足为D,若OA=OB=OD=1
(1)写出点A,B,D的坐标; (2)求一次函数和反比例函数的解析式;
21. (10分) 已知一次函数y=2x+k-3和反比例函数 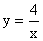 的图象都经过点A(n,2)
(1)求n的值和一次函数的解析式;
的图象都经过点A(n,2)
(1)求n的值和一次函数的解析式;
(2)在直角坐标系中画出这两个函数的大致图象; (3)根据图象判断:使这两个函数值都为非负数的自变量x的取值范围是什么?
A. y=x B. 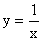 C. y=2x+1 D.
C. y=2x+1 D. 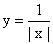 7.反比例函数
7.反比例函数  的图象在第二、四象限,则一次函数y=kx-5的图象不经过
( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
8. 已知反比例函数
的图象在第二、四象限,则一次函数y=kx-5的图象不经过
( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
8. 已知反比例函数  ,当x<0时,y随x的增大而增大,那么一次函数y=kx-k的图象经过( )
A. 第三、二、一象限 B. 第二、一、四象限
C. 第三、四、一象限 D. 第二、三、四象限
9.反比例函数
,当x<0时,y随x的增大而增大,那么一次函数y=kx-k的图象经过( )
A. 第三、二、一象限 B. 第二、一、四象限
C. 第三、四、一象限 D. 第二、三、四象限
9.反比例函数 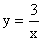 与直线y=3x相交,那么交点的坐标为( )
A.(1,3) B.(-1,-3) C.(1,3)或(-1,-3) D. (2,3)或(-2,-3)
10.面积为2的△ABC,一边长为x,这边上的高为y,则y与x的变化规律用图象表示大致是( )
与直线y=3x相交,那么交点的坐标为( )
A.(1,3) B.(-1,-3) C.(1,3)或(-1,-3) D. (2,3)或(-2,-3)
10.面积为2的△ABC,一边长为x,这边上的高为y,则y与x的变化规律用图象表示大致是( )
 二、填空题(每小题3分,共24分)
11. 已知函数y=kx的图象经过点(2,-6),则函数
二、填空题(每小题3分,共24分)
11. 已知函数y=kx的图象经过点(2,-6),则函数  的解析式可确定为_____
12. 已知函数
的解析式可确定为_____
12. 已知函数 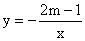 的图象在第一、三象限,则m的取值范围为____
13. 反比例函数
的图象在第一、三象限,则m的取值范围为____
13. 反比例函数  的图象经过点
的图象经过点 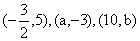 ,则k=___,a=____,b=____
,则k=___,a=____,b=____
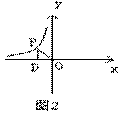 14.如图2,点P是反比例函数
14.如图2,点P是反比例函数
 上的一点,PD垂直x轴
上的一点,PD垂直x轴
于点D,则△POD的面积为____
15.已知反比例函数 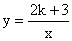 的图象在第一、三象限,反比例函数
的图象在第一、三象限,反比例函数 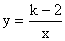 的值在x>0时随x的增大而增大,则k的取值范围是____
16. 函数y=(2m-1)x与
的值在x>0时随x的增大而增大,则k的取值范围是____
16. 函数y=(2m-1)x与  的图象交于一、三象限,则m的取值范围是____
17.反比例函数
的图象交于一、三象限,则m的取值范围是____
17.反比例函数 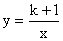 ,点(x1,y1),(x2,y2)在其图象上,当x1<0<x2时,有y1>y2,则k的取值范围是_______
18. 为了美化校园,学校共划出84m2的土地修建四个完全相同的长方形花坛,如果每个花坛的一组邻边分别为xcm,ycm,那么y关于x的函数关系式为____
三、解答题 (共26分)
19.(6分)在反比例函数
,点(x1,y1),(x2,y2)在其图象上,当x1<0<x2时,有y1>y2,则k的取值范围是_______
18. 为了美化校园,学校共划出84m2的土地修建四个完全相同的长方形花坛,如果每个花坛的一组邻边分别为xcm,ycm,那么y关于x的函数关系式为____
三、解答题 (共26分)
19.(6分)在反比例函数  的图象上有一点P,它的横坐标是方程-2t-2=0的解,纵坐标是直线y=2x+3与y轴交点的纵坐标,由此,请你求出这个反比例函数的解析式。
的图象上有一点P,它的横坐标是方程-2t-2=0的解,纵坐标是直线y=2x+3与y轴交点的纵坐标,由此,请你求出这个反比例函数的解析式。
20.(10分)已知一次函数y=x+m与反比例函数 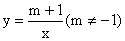 的图象在第一象限内的交点为P(a,3)
(1)求a的值;
(2)求一次函数和反比例函数的解析式。
的图象在第一象限内的交点为P(a,3)
(1)求a的值;
(2)求一次函数和反比例函数的解析式。
18.在压力不变的情况下,某物体承受的压强p(Pa)是它的受力面积S (m2)的反比例函数,其图像如图所示.

(l)求p与S之间的函数关系式;
(2)求当S=0.5m2时物体承受的压强P.
17.已知反比例函数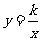 (k≠0)和一次函数y=-x-6
(k≠0)和一次函数y=-x-6
(1)若一次函数和反比例函数的图像交于点(-3,m),求m和k的值;
(2)当k满足什么条件时,这两个函数的图像有两个不同的交点?
(3)当k=-2时,设(2)中的两个函数图像的交点分别为A、B,试判断此时A、B两点分别在第几象限?∠AOB是锐角还是钝角?(只要求直接写出结论)
16. 如图,一次函数y=-ax-b的图像与反比例函数
如图,一次函数y=-ax-b的图像与反比例函数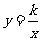 的图象交
的图象交
于M、N两点.
(l)求反比例函数和一次函数的解析式;
(2)根据图像写出使反比例函数的值大于一次函数的值的x的
取值范围.
15.如图,一次函数y=kx+b的图像与反比例函数y= 的图像交于A、B两点:A(-2,l)、B(l,n).
的图像交于A、B两点:A(-2,l)、B(l,n).
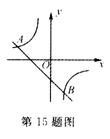 (l)求反比例函数和一次函数的解析式;
(l)求反比例函数和一次函数的解析式;
(2)根据图像写出使一次函数的值大于反比例函数的值的x取值范围.
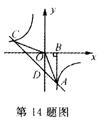
14.如图,Rt△ABO的顶点A是双曲线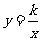 与直线y=-x+(k+1)在第四
与直线y=-x+(k+1)在第四
象限的 交点, AB⊥x轴于B 且SAOC= ,
,
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A、C的坐标和△AOC的面积.
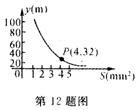 12.(05济南)你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)S(mm2)的反比例函数,其图像如图所示.
12.(05济南)你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)S(mm2)的反比例函数,其图像如图所示.
(1)写出y与S的函数关系式;
(2)求当面条粗1.6mm2时,面条的总长度是多少米?
13.已知一次函数y=x+m与反比例函数y=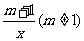 ,的图像在第一象限内的交点为P(x0,3).
,的图像在第一象限内的交点为P(x0,3).
(1)求x0的值
(2)求一次函数和反比例函数的解析式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com