
17、解:依题意可得: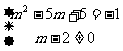 ;解得:
;解得:
∴当 时,函数y=(m-2)
时,函数y=(m-2)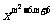 是反比例函数;当
是反比例函数;当 时,代入可得:
时,代入可得: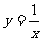 ;∵
;∵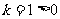 ,∴它的图象位于第一、第三象限。
,∴它的图象位于第一、第三象限。
由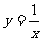 可得
可得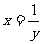 ,∵
,∵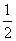 ≤x≤2;∴
≤x≤2;∴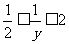 ;解得:
;解得: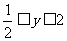 。
。
16、16
11、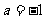 12、
12、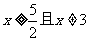 13、
13、 14、
14、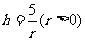 15、(仅供参考)如:当路程s一定时,速度v是时间t的反比例函数;函数关系式为v=
15、(仅供参考)如:当路程s一定时,速度v是时间t的反比例函数;函数关系式为v=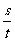 (s是常数)
(s是常数)
17(9分)设函数y=(m-2)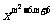 ,当m取何值时,它是反比例函数?它的图象位于哪些象限?求当
,当m取何值时,它是反比例函数?它的图象位于哪些象限?求当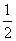 ≤x≤2时函数值y的变化范围.
≤x≤2时函数值y的变化范围.
|
18(9分)已知甲、乙两站的路程是312
km,一列列车从甲站开往乙站,设列车的平均速度为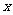 km/h,所需时间为
km/h,所需时间为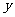 h。
h。
(1)试写出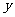 关于
关于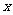 的函数关系式;
的函数关系式;
(2)2006年全国铁路第六次大提速前,这列列车从甲站到乙站需要4 h,列车提速后,速度提高了26 km/h,问提速后从甲站到乙站需要几个小时?
19(10分)已知一次函数y=x+m与反比例函数y=
(m≠-1)的图象在第一象限内的交点为P(x0,3).
(1)求x0的值;
(2)求一次函数和反比例函数的解析式.
20(10分)、已知函数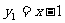 和
和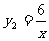 。
。
(1)在所给的19题图的坐标系中画出这两个函数的图象。
(2)求这两个函数图象的交点坐标。
(3)观察图象,当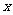 在什么范围时,
在什么范围时,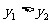 ?
?
解: :
21(12分)、已知正比例函数y=4x,反比例函数y=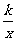 .
.
求:(1)k为何值时,这两个函数的图象有两个交点?k为何值时,这两个函数的图象没有交点?
(2)这两个函数的图象能否只有一个交点?若有,求出这个交点坐标;若没有,请说明理由.
22(12分)、已知y=y1+y2 ,y1与x+1成正比例,y2与x+1成反比例,当x=0时,y=-5;当x=2时,y=-7。
(1)求y与x的函数关系式;
(2)当y=5时,求x的值。
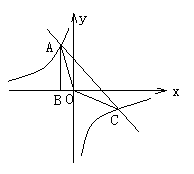
23(12分)、如图,Rt△ABO的顶点A是双曲线y=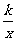 与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=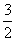 .
.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A、C的坐标和△AOC的面积.
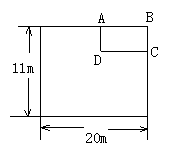
24(14分)某单位为响应政府发出的全民健身的号召,打算在长和宽分别为20m和11m的矩形大厅内修建一个60m2的矩形健身房ABCD. 该健身房的四面墙壁中有两侧沿用大厅的旧墙壁(如图为平面示意图),已知装修旧墙壁的费用为20元/m2,新建(含装修)墙壁的费用为80元/m2.设健身房的高为3m,一面旧墙壁AB 的长为xm,修建健身房墙壁的总投入为y元.
(1)求y与x的函数关系式;
(2)为了合理利用大厅,要求自变量x必须满足条件:8≤x≤12, 当投入的资金为4800元时,问利用旧墙壁的总长度为多少?
25(14分)、如图所示,点A、B在反比例函数y=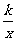 的图象上,且点A、B的横坐标分别为a、2a(a>0),AC⊥x轴于点C,且△AOC的面积为2.
的图象上,且点A、B的横坐标分别为a、2a(a>0),AC⊥x轴于点C,且△AOC的面积为2.
(1)求该反比例函数的解析式.
(2)若点(-a,y1)、(-2a,y2)在该函数的图象上,试比较y1与y2的大小.
 (3)求△AOB的面积.
(3)求△AOB的面积.
附答案:
16、若A、B两点关于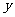 轴对称,且点A在双曲线
轴对称,且点A在双曲线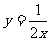 上,点B在直线
上,点B在直线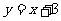 上,设点A的坐标为(a,b),则
上,设点A的坐标为(a,b),则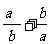 =
。
=
。
15、我们学习过反比例函数.例如,当矩形面积S一定时,长a是宽b 的反比例函数,其函数关系式可以写为a=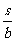 (S为常数,S≠0).
(S为常数,S≠0).
请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数关系的量的实例,并写出它的函数关系式.
实例:______________________________________________________________;
函数关系式:_______________________
14、.已知圆柱的侧面积是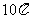
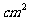 ,若圆柱底面半径为
,若圆柱底面半径为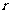
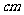 ,高为
,高为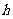
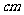 ,则
,则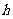 与
与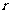 的函数关系式是
。
的函数关系式是
。
13、在反比例函数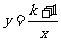 的图象上有两点
的图象上有两点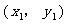 和
和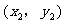 ,若
,若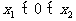 时,
时,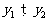 ,则
,则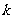 的取值范围是 .
的取值范围是 .
12、在函数y= +
+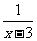 中自变量x的取值范围是_________.
中自变量x的取值范围是_________.
11、已知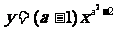 是反比例函数,则a=____ .
是反比例函数,则a=____ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com