2．反比例函数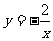，当x＝－2时，y＝　　　 ；当x＜－2时；y的取值范围是　　 ；

当x＞－2时；y的取值范围是　　

1．若函数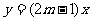与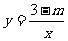的图象交于第一、三象限，则m的取值范围是　　

3．在平面直角坐标系内，过反比例函数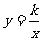(k＞0)的图象上的一点分别作x轴、y轴的垂线段，与x轴、y轴所围成的矩形面积是6，则函数解析式为　　　　　

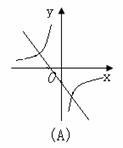
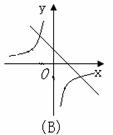
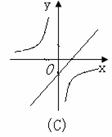
2．函数y＝－ax+a与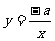(a≠0)在同一坐标系中的图象可能是(　　 )

1．已知反比例函数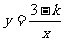，分别根据下列条件求出字母k的取值范围

(1)函数图象位于第一、三象限

(2)在第二象限内，y随x的增大而增大

例2．见教材P48，用描点法画图，注意强调：

(1)列表取值时，x≠0，因为x＝0函数无意义，为了使描出的点具有代表性，可以“0”为中心，向两边对称式取值，即正、负数各一半，且互为相反数，这样也便于求y值

(2)由于函数图象的特征还不清楚，所以要尽量多取一些数值，多描一些点，这样便于连线，使画出的图象更精确

(3)连线时要用平滑的曲线按照自变量从小到大的顺序连接，切忌画成折线

(4)由于x≠0，k≠0，所以y≠0，函数图象永远不会与x轴、y轴相交，只是无限靠近两坐标轴

例1．(补充)已知反比例函数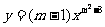的图象在第二、四象限，求m值，并指出在每个象限内y随x的变化情况？

分析：此题要考虑两个方面，一是反比例函数的定义，即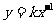(k≠0)自变量x的指数是－1，二是根据反比例函数的性质：当图象位于第二、四象限时，k＜0，则m－1＜0，不要忽视这个条件

略解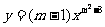：∵是反比例函数　　　　 ∴m²－3＝－1，且m－1≠0

　又∵图象在第二、四象限　　　　 ∴m－1＜0

解得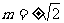且m＜1　　　 则

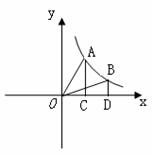例2．(补充)如图，过反比例函数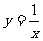(x＞0)的图象上任意两点A、B分别作x轴的垂线，垂足分别为C、D，连接OA、OB，设△AOC和△BOD的面积分别是S₁、S₂，比较它们的大小，可得(　　　 )

(A)S₁＞S₂　　　　 (B)S₁＝S₂ 　　

(C)S₁＜S₂　　　　 (D)大小关系不能确定

分析：从反比例函数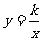(k≠0)的图象上任一点P(x，y)向x轴、y轴作垂线段，与x轴、y轴所围成的矩形面积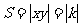，由此可得S₁＝S₂ ＝ ，故选B

3．反比例函数的图象是什么样呢?

2．画函数图象的方法是什么?其一般步骤有哪些？应注意什么？

提出问题：

1．一次函数y＝kx+b(k、b是常数，k≠0)的图象是什么？其性质有哪些？正比例函数y＝kx(k≠0)呢？

教材第48页的例2是让学生经历用描点法画反比例函数图象的过程，一方面能进一步熟悉作函数图象的方法，提高基本技能；另一方面可以加深学生对反比例函数图象的认识，了解函数的变化规律，从而为探究函数的性质作准备。

补充例1的目的一是复习巩固反比例函数的定义，二是通过对反比例函数性质的简单应用，使学生进一步理解反比例函数的图象特征及性质。

补充例2是一道典型题，是关于反比例函数图象与矩形面积的问题，要让学生理解并掌握反比例函数解析式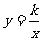(k≠0)中的几何意义。