
7.直角三角形中一直角边的长为9,另两边为连续自然数,则直角三角形的周长为( )
A.121 B.120 C.90 D.不能确定
6.已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是( )
A. 24cm2 B. 36cm2 C. 48cm2 D. 60cm2
5.已知一个直角三角形的两边长分别为3和4,则第三边长是( )
A.5 B.25 C.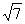 D.5或
D.5或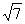
4. 三角形的三边长为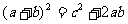 ,则这个三角形是( )
,则这个三角形是( )
A. 等边三角形 B. 钝角三角形 C. 直角三角形 D. 锐角三角形.
3. 三角形的三边为a、b、c,由下列条件不能判断它是直角三角形的是( )
A.a:b:c=8∶16∶17 B. a2-b2=c2
C.a2=(b+c)(b-c) D. a:b:c =13∶5∶12
2. 下面几组数:①7,8,9;②12,9,15;③m2 + n2, m2–n2, 2mn(m,n均为正整数,m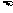 n);④
n);④ ,
,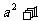 ,
, .其中能组成直角三角形的三边长的是( )
.其中能组成直角三角形的三边长的是( )
A. ①② B. ②③ C. ①③ D. ③④
1. 三角形的三边长分别为6,8,10,它的最短边上的高为( )
A. 6 B. 4.5 C. 2.4 D. 8
25.(10分)如图,A市气象站测得台风中心在A市正东方向300千米的B处,以10 千米/时的速度向北偏西60°的BF方向移动,距台风中心200千米范围内是受台风影响的区域.
千米/时的速度向北偏西60°的BF方向移动,距台风中心200千米范围内是受台风影响的区域.
(1)A市是否会受到台风的影响?写出你的结论并给予说明;
(2)如果A市受这次台风影响,那么受台风影响的时间有多长?

答案:
1.B 2.D 3.D 4.C 5.A 6.D 7.A 8.A 9.A 10.B
11.5或 12.1.5 13.600
12.1.5 13.600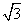 14.1 15.2 16.略 17.AD
14.1 15.2 16.略 17.AD
18.BCD 19.树高15m. 提示:BD=x,则(30-x)2-(x+10)2=202
20.连结AE,则△ADE≌△AFE,所以AF=AD=10,DE=EF.
设CE=x,则EF=DE=8-x,BF= =6,CF=4.
=6,CF=4.
在Rt△CEF中,EF2=CE2+CF2,即(8-x)2=x2+16,故x=3
21.当CD为斜边上的高时,CD最短,从而水渠造价最价
∵CD·AB=AC·BC ∴CD=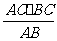 =48米
=48米
∴AD=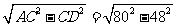 =64米
=64米
所以,D点在距A点64米的地方,水渠的造价最低,其最低造价为480元.
22.(1)Sn=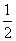
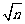 ·1=
·1=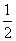
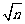 (2)OA10=
(2)OA10=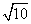
(3)S12+S22+…+S102=(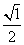 )2+(
)2+(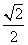 )2+(
)2+(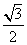 )2…+(
)2…+(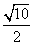 )2
)2
=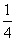 (1+2+…+10)=
(1+2+…+10)=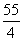 .
.
23.(1)①S△ABQ=S△BCM=S△CDN=S△ADP=6
②S正方形ABCD=S正方形MNPQ-4S△ABQ=25
(2)勾股定理或完全平方公式或平方差公式,推理过程略.
24.(1)设直角三角形的两条边分别为a、b(a>b),则依题意有:
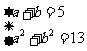 ①2-②,得ab=6,(a-b)2=(a+b)2-4ab=1,
①2-②,得ab=6,(a-b)2=(a+b)2-4ab=1,
∴a-b=1,故小正方形的面积为1.
(2)

25.(1)过A作AC⊥BF于C,则AC=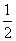 AB=150<200,
AB=150<200,
∴A市会受到台风影响.
(2)过A作AD=200km,交BF于点D.
∴DC= =50
=50 ,
,
∴该市受台风影响的时间为: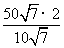 =10小时.
=10小时.
24.(12分)(1)四年一度的国际数学家大会于2002年8月20日在北京召开,大会会标如图(1).它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积为13,每个直角三角形两直角边的和是5,求中间小正方形的面积.
(2)现有一张长为6.5cm,宽为2cm的纸片,如图(2),请你将它分割成6块,再拼合成一个正方形.
(要求:先在图(2)中画出分割线,再画出拼成的正方形并标明相应数据)

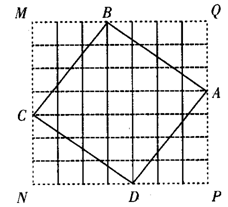
23.(9分)如图,正方形MNPQ网格中,每个小方格的边长都相等,正方形ABCD的顶点在正方形MNPQ的4条边的小方格顶点上.
(1)设正方形MNPQ网格内的每个小方格的边长为1,求:
①△ABQ,△BCM,△CDN,△ADP的面积;
②正方形ABCD的面积.
(2)设MB=a,BQ=b,利用这个图形中的直角三角形和正方形的面积关系,你能验证已学过的哪一个数学公式或定理吗?相信你能给出简明的推理过程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com