课本第60页复习题A组的1、2、3、4，B组的12、13。

第二课时　 回顾与思考(二)

教学目标

使学生掌握一次函数、反比例函数的图象和性质，掌握这两个函数中的系数对图象的影响，能用待定系数法确定这两个函数的解析式，进一步体会方程与函数的关系，正确画出这两个函数的图象，能从图象中获取信息，灵活运用所学的知识解决问题。

教学教程

本节课由于复习的知识多且零散，要求同学们在深刻理解的基础上加强记忆，并且做到灵活应用所学的知识解决问题．

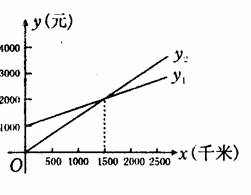
5．某单位急需用车，但又不准备买车，他们准备和一个体车或一国营出租车公司的一家签定月租车合同，设汽车每月行驶x千米，应付给个体车主的月费用是y₁元，应付给出租车公司的月费是y₂元，y_l、y₂分别与工之间的函数关系图象 (两条射线)如下图所示，观察图象回答下列问题：

　　 (1)每月行驶的路程在什么范围内，租国营公司的车合算?　　

　　 (2)每月行驶的路程等于多少时，租两家的费用相同?　　

(3)如果这个单位估计每月行驶的路程为2300千米，那么这个单位租哪家公司的车比较合算?

4．(1)若M(a－2，－a+3)在x轴上，则a＝(　　)；

　　 (2)若M(a－2，－a+3)在第三象限，则a的取值范围是(　　)；

　　 (3)若M(a－2，－a+3)在第一、三象限的角平分线上，则a＝ (　　)；

　　 (4)求M(a－2，－a+3)在关于y轴对称的点的坐标是(　)；

3．平行四边形的底边为5，则其面积S与底边上的高h之间的函数关系式是

2．求下列函数的自变量取值范围

　　y＝　 y＝　y＝

1．x²－3x－4是x的函数吗?为什么?

4．函数的图象

函数的图象是由直角坐标系中的一系列点组成，图象上的每一点坐标(x，y)代表了函数的一对对应值，即把自变量x与函数y的每一对对应值分别作为点的横坐标和纵坐标，在直角坐标系中描出相应的点，这些点组成的图形，就是这个函数的图象。

3．关于平面直角坐标系

　　 (1)平面上的点与有序实数对成一一对应关系，其含义是坐标平面上的每一个点都可以用一对有序实数来表示，反过来，每一对有序实数都可以在坐标平面上描出一点，这样数与形就有机地结合在一起。我们可以在平面上建立直角坐标系定出点的位置。

　　 (2)关于x轴、y轴、原点对称的点的坐标间具有什么关系?

　　 (3)各个象内的点的横、纵坐标的符号是怎样的?

　　 (4)点落在坐标轴上，它的坐标有什么特点?

2、如何求函数的自变量取值范围

　　 考虑两个方面，其一是分母不等于0，其二是开偶次方的被开方数为非负数，对于实际问题，应根据具体情况而定。