2．求函数自变量取值范围的两个方法(依据)：

　(1)要使函数的解析式有意义．

　①函数的解析式是整式时，自变量可取全体实数；

　②函数的解析式是分式时，自变量的取值应使分母≠0；

　③函数的解析式是二次根式时，自变量的取值应使被开方数≥0．

　(2)对于反映实际问题的函数关系，应使实际问题有意义．

1．解析法的意义：用数学式子表示函数的方法叫解析法．

4．讲解例题，求下列函数当x=2时的函数值：

　(1)y=2x－5； 　　 (2)y=－3x²；

　结合例题引出函数值的意义．并指出两点：

　(1)例题中的4个小题归纳起来仍是三类题型．

　(2)求函数值的问题实际是求代数式值的问题．

　课堂练习:

　求下列函数当x=3时的函数值：

　(1)y=6x－4；(2)y=－5x²；

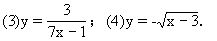
　小结

3．讲解例题，求下列函数中自变量x的取值范围，并指出四个小题代表三类题型：

　(1)y=2x+3； 　　　(2)y=－3x²；

　(1)，(2)题给出的是只含有一个自变量的整式；(3)题给出的是只含有一个自变量的分式；(4)题给出的是只含有一个自变量的二次根式．

2．结合同学举出的实例，说明函数的自变量取值范围有时要受到限制．这就可以引出自变量取值范围的意义，并说明求自变量的取值范围的两个依据是：

　(1)自变量取值范围是使函数解析式(即是函数表达式)有意义．

　(2)自变量取值范围要使实际问题有意义．

1．结合同学举出的实例说明解析法的意义：用数学式子表示函数的方法叫解析法．并指出，函数表示法除了解析法外，还有图象法和列表法．

3．举出一个函数的实例，并指出式中的变量与常量、自变量与函数．

　新课

2．什么叫二次根式？使二次根式成立的条件是什么？(答：根指数是2的根式叫二次根式，使二次根式成立的条件是被开方数≥0．)

　复习提问

1．函数的定义是什么？函数概念包含哪三个方面的内容？　

　重点：函数自变量取值的求法．

　难点：函数自变量取值的确定．