2．数轴上的点与实数间的关系是什么？(一一对应关系，即数轴上每一个点的位置都能用一个实数表示，反之，任何一个实数在数轴上都有唯一的一个点和它对应，这个实数叫做这个点在数轴上的坐标)．

　引导学生回忆：

1．什么是数轴？(规定了原点，正方向及长度单位的直线)

2.　 你能看出这一天的最高气温与最低气温是多少吗

1.　 你能看此8时,12时,18时的气温各是多少吗?

2．掌握平面内的点与有序实数对的一一对应关系，并能熟练地根据坐标找出平面内的点，由点求得坐标．

　教学重点和难点

　使学生掌握x轴和y轴上的点及四个象限内点的坐标具有的特征，平行x轴和y轴的直线上的点和第一、三象限角平分线，第二、四象限角平分线上点的坐标的特征，使学生懂得建立了平面直角坐标系，就使平面上的点与一对有序实数之间建立起一一对应关系，这就建立了“数”与“形”之间的联系．

　教学过程

引入:

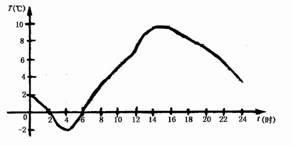
如上图

1．使学生理解平面直角坐标系的意义，会建立直角坐标系．

3．注意培养学生对于“具体问题要具体分析”的良好学习方法．比如对于有实际意义的函数，自变量的取值范围应根据实际意义来确定，由于实际问题千差万别，所以我们就要具体分析，灵活处置．

平面直角坐标系(一)

　教学目的

2．注意训练与培养学生的优质联想能力．要求学生仿照例题自编题目是有效手段．

1．注意渗透与训练学生的归纳思维．比如例3、例4中各是4个小题，对每一个例题均可归纳为三类题型．而对于例3、例4这两道例题，虽然要求各异，但题目结构仍是三类题型：整式、分式、二次根式．

3．求函数值的方法：把所给出的自变量的值代入函数解析式中，即可求出相应的函数值．

　练习：选用课本练习

　作业：选用课本练习