
创设情境,引入课题
[]
前面我们己学习了一次函数的概念,一般地,如果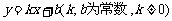 ,那么
,那么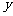 叫
叫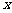 的一次函数。特别地:当
的一次函数。特别地:当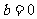 时,一次函数就变成了正比例函数
时,一次函数就变成了正比例函数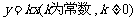 。
。
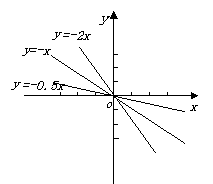
在同一直角坐标系中投影出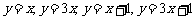 的函数图象,让学生观察它们的图象都是直线并引入课题。
的函数图象,让学生观察它们的图象都是直线并引入课题。
所有的一次函数的图象都是直线。因此要画一次函数的图象--一条直线,就没有必要把所有的点都描出来,只要描出两个点就可以了,因为两个点确定一条直线。利用这个结论,我们可以更快地作出一次函数的图象,并对它的性质进行研究。
描点画图,归纳画法
[过渡]下面我们一起来画首先共同画出正比例函数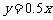 与
与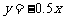 的图象。并由此归纳出正比例函数
的图象。并由此归纳出正比例函数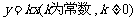 的图象为过
的图象为过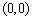 和
和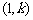 两点的直线。
两点的直线。
观察图象、研究性质
然后提出问题1:让学生自己画图,研究正比例函数有何性质?即正比例函数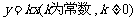 中,
中,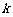 对函数图象有何影响?并填写实验报告(课前印好发给学生,或者学生在网络上填写)。
对函数图象有何影响?并填写实验报告(课前印好发给学生,或者学生在网络上填写)。
研究问题1时,我首先通过几何画板与学生共同归纳正比例函数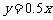 与
与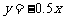 的图象性质,特别是
的图象性质,特别是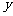 随
随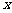 的变化趋势。
的变化趋势。
打开几何画板,进行演示。点在直线上运动,对应着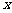 轴上射影(用红点显示)、
轴上射影(用红点显示)、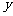 轴上的射影(用绿点显示)同时运动。从左到右拖动红点,使点的横坐标从小到大变化,红点的运动引起绿点的运动,绿点的运动又使点的纵坐标发生变化。在演示的同时,启发学生注意观察坐标的变化并得到:对于
轴上的射影(用绿点显示)同时运动。从左到右拖动红点,使点的横坐标从小到大变化,红点的运动引起绿点的运动,绿点的运动又使点的纵坐标发生变化。在演示的同时,启发学生注意观察坐标的变化并得到:对于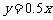 ,
,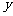 随
随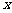 的增大而增大;对于
的增大而增大;对于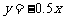 ,
,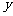 随
随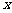 的增大而减小。
的增大而减小。
然后把学生分成两人一组,让他们进行继续用几何画板研究其它正比例函数的性质,并把结论发到网络的“展示区”上。填写实验报告如下:
实验报告: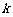 对正比例函数
对正比例函数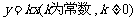 的图象的影响。
的图象的影响。
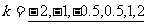
|
|
解析式 |
图象示意图 |
图象所在的象限 |
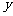 随 随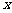 的变化趋势 的变化趋势 |
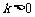 |
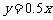 |
在刚才所画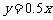 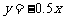 直角坐标系中分别画出,图象如下所示。 直角坐标系中分别画出,图象如下所示。 |
1,3象限 |
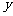 随 随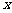 的增大而增大 的增大而增大 |
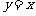 |
1,3象限 |
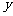 随 随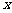 的增大而增大 的增大而增大 |
||
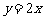 |
1,3象限 |
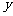 随 随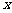 的增大而增大 的增大而增大 |
||
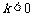 |
 |
2,4象限 |
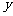 随 随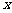 的增大而减小 的增大而减小 |
|
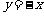 |
2,4象限 |
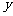 随 随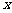 的增大而减小 的增大而减小 |
||
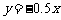 |
2,4象限 |
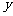 随 随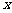 的增大而减小 的增大而减小 |
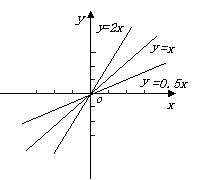
在实验报告的基础上,我让学生利用几何画板动手实验:拖动点N,让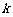 的值连续变化,引导学生观察正比例
的值连续变化,引导学生观察正比例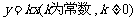 的图象的变化并归纳出它的性质:
的图象的变化并归纳出它的性质:
当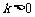 时,图象在1,3象限,
时,图象在1,3象限,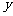 随
随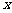 的增大而增大;
的增大而增大;
当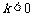 时,图象在2,4象限,
时,图象在2,4象限,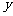 随
随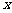 的增大而减小。
的增大而减小。
为了达到及时巩固的效果,归纳之后进行练习1。练习1结合课本练习,培养学生的数形结合能力。
第1、2、3题都是由函数解析式判断图象的性质;
第4题是由函数图象性质判断函数的解析式。
并通过填空、选择的形式,让学生进行自我评价。(1)做完练习1后,会显示每道题目的答案正确与否,同时根据学生练习完成的情况,给出鼓励性评价;(2)老师可以对全体学生练习情况进行即时统计,从而进行针对性教学;(3)练习完成的好的学生可以进入英雄榜,让学生更乐于学习。
类比联想、探索性质
首先学习例3:在同一直角坐标系中画出 与
与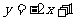 的图象。在画图的过程中利用表格(如下):
的图象。在画图的过程中利用表格(如下):
|
解析式 |
与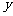 轴的交点 轴的交点 |
与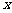 轴的交点 轴的交点 |
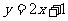 |
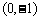 |
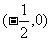 |
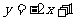 |
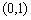 |
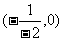 |
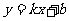 |
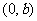 |
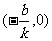 |
归纳出一次函数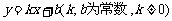 为过
为过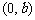 和
和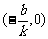 两点的直线。
两点的直线。
然后提出问题2:讨论一次函数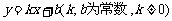 中,
中,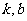 对函数图象有何影响?
对函数图象有何影响?
在解决问题2时,首先抓住正比例函数是一次函数的特殊情况,让学生了解这一关系并从中直接得出一次函数性质。
然后利用网络让学生动手实验:
先固定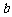 的值,拖动滑板,让
的值,拖动滑板,让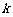 的值连续变化,观察图象的变化,归纳出一次函数
的值连续变化,观察图象的变化,归纳出一次函数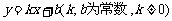 的性质:
的性质:
当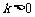 时,
时,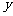 随
随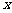 的增大而增大;
的增大而增大;
当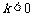 时,
时,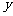 随
随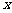 的增大而减小。
的增大而减小。
再固定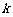 的值,拖动滑板,让
的值,拖动滑板,让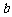 的值连续变化,观察图象的变化,归纳出
的值连续变化,观察图象的变化,归纳出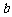 的变化引起图象变化规律:一次函数
的变化引起图象变化规律:一次函数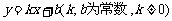 图象与
图象与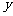 轴的交点为
轴的交点为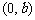 。
。
练习反馈、巩固性质
为了加强学生对“数”与“形”的双向沟通,我在课本练习基础上设计了一些“由数到形”及“由形到数”的题目,供学生练习。练习2采用题组分层次教学,先后通过A、B、C三组(9题)进行练习,每组题均由浅入深,各有针对性。
A组题为只考虑一个常数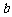 的题目;
的题目;
B组题为只考虑一个常数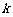 的题目;
的题目;
A、B两组题为必做题;
C组综合考虑两个常数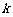 与
与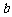 的题目,C组题为选做题。
的题目,C组题为选做题。
这样遵循循序渐进的规律进行题组教学,顾及到了各个层次的学生,达到了预期的目的。
小结归纳,揭示规律
先由学生归纳,再由老师总结,培养学生的归纳能力。
(1)正比例函数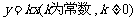 的图象的画法:过原点与点
的图象的画法:过原点与点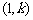 的直线即所求的图象;
的直线即所求的图象;
(2)一次函数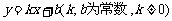 图象的画法:在
图象的画法:在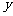 轴上取点
轴上取点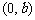 ,在
,在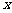 轴上取点
轴上取点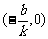 ,过这两点的直线即所求的图象;
,过这两点的直线即所求的图象;
(3)正比例函数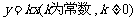 与一次函数
与一次函数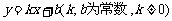 的性质。
的性质。
一次函数的图象和性质(二)
“实践探究、启发引导、归纳概括” 的引导探究法
教学重点
一次函数的图象与性质
教学难点
对一次函数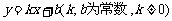 中
中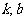 的数与形的联系的理解
的数与形的联系的理解
知识目标
使学生掌握利用两个适当的点画出一次函数的图象;
和结合图象,使学生理解掌握一次函数的性质;
能力目标
探索新问题的能力,动手能力及现代化操作技术能力。
思想方法目标
初步了解数形结合
1. 通过本节课的学习,你学到了哪些知识?研究过程中用到了什么数学思想?
现实生活中有哪些实际问题涉及到一次函数与正比例函数的知识?请你举几例(尽可能是以上我们没有提到过的!)
一次函数的图象与性质(一)
1.已知,4y+3m与2x-5n成正比例,证明y是x的一次函数。
㈢.反思题:
2.从A地向B地打长途电话,按时收费,3分钟收费2.4元,每加1分钟收1元,求时间t≥3(分)时电话费y(元)与t之间的函数关系式。
㈡.选作题(C组)
C组:
1.汽车由天津驶往相距120千米的北京,它的平均速度是30千米/时,求汽车距北京的路程s(千米)与行驶时间t(小时)的函数关系式,写出自变量取值范围。
2.一水库现蓄水am3,从开闸放水起,每小时放水bm3,同时从上游每小时流入水库am3水,则水库蓄水量y(m3)与开闸时间t(时)之间的函数关系式是----------------。
B组:
1.某种储蓄的月利率是0.6%,存入100元本金,本息和(本金与利息三和)y(元)与所存月数x之间的函数关系式是--------;4个月后的本息和为--------。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com