
看上面问题的图,回答下列问题:
(1)小强让爷爷先上多少米?
(2)山顶离山脚的距离有多少米?谁先爬上山顶?
分析 (1)小强让爷爷先跑的路程,应该看表示爷爷的这条线段.由于从小强开始爬山时计时的,因此这时爷爷爬山所用时间是0,而x轴表示爬山所用时间,得x=0.可在线段上找到这一点A(如图).A点对应的函数值y=60.
(2) y轴表示离开山脚的距离,山顶离山脚的距离指的是离开山脚的最大距离,也就是函数值y取最大值.可分别在这两条线段上找到这两点B、C(如图),过B、C两点分别向x轴、y轴作垂线,可发现交y轴于同一点Q(因为两人爬的是同一座山), Q点的数值就是山顶离山脚的距离,分别交x轴于M、N,M、N点的数值分别是小强和爷爷爬上山顶所用的时间,比较两值的大小就可判断出谁先爬上山顶.
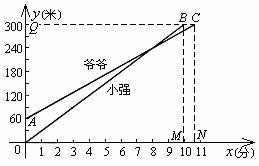
解 (1)小强让爷爷先上60米;
(2)山顶离山脚的距离有300米,小强先爬上山顶.
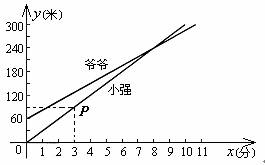
归纳 在观察实际问题的图象时,先从两坐标轴表示的实际意义得到点的坐标意义.如图中的点P(3,90),这一点表示小强爬山3分后,离开山脚的距离90米.再从图形中分析两变量的相互关系,寻找对应的现实情境.如图中的两条线段都可以看出随着自变量x的逐渐增大,函数值y也随着逐渐增大,再联系现实情境爬山所用时间越长,离开山脚的距离越大,当x达到最大值时,也就是到达山顶.
问题 王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(从小强开始爬山时计时).
问 图中有一个直角坐标系,它的横轴(x轴)和纵轴(y轴)各表示什么?
答 横轴(x轴)表示两人爬山所用时间,纵轴(y轴)表示两人离开山脚的距离.
问 如图,线段上有一点P,则P的坐标是多少?表示的实际意义是什么?
答 P的坐标是(3,90).表示小强爬山3分后,离开山脚的距离90米.
我们能否从图象中看出其它信息呢?
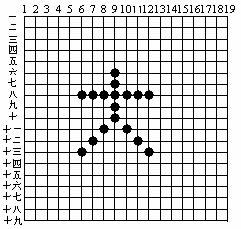
5.如图是一个围棋棋盘,我们可以用类似于直角坐标系的方法表示各个棋子的位置.例如,图中右下角的一个棋子可以表示为(12,十三).请至少说出图中四个棋子的“位置”.
4.填空:
(1)点P(5,-3)关于x轴对称点的坐标是 ;
(2)点P(3,-5)关于y轴对称点的坐标是 ;
(3)点P(-2,-4)关于原点对称点的坐标是 .
3.指出下列各点所在的象限或坐标轴:
A(-3,-5),B(6,-7),C(0,-6),D(-3,5),E(4,0).
2.在直角坐标系中描出下列各点,顺次用线段将这些点连起来,并将最后一点与第一点连起来,看看得到的是一个什么图形?
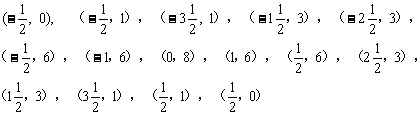
1.判断下列说法是否正确:
(1)(2,3)和(3,2)表示同一点;
(2)点(-4,1)与点(4,-1)关于原点对称;
(3)坐标轴上的点的横坐标和纵坐标至少有一个为0;
(4)第一象限内的点的横坐标与纵坐标均为正数.
4.分别关于x轴、y轴及原点的对称的两点坐标之间的关系.
3.在四个象限内的点的坐标特征;两条坐标轴上的点的坐标特征;第一、三象限角平分线上点的坐标特征;第二、四象限角平分线上点的坐标特征;
2.在直角坐标系中,根据坐标找出点;由点求出坐标的方法;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com