3.平面直角坐标系中，x轴、y轴上的点的坐标有什么特征？

2.正比例函数y＝kx(k≠0)的图象是经过哪一点的直线？

(正比例函数y＝kx(k≠0)的图象是经过原点(0，0)的一条直线).

1.一次函数的图象是什么，如何简便地画出一次函数的图象？

(一次函数y＝kx+b(k≠0)的图象是一条直线，画一次函数图象时，取两点即可画出函数的图象).

5.按照我国税法规定：个人月收入不超过800元，免交个人所得税．超过800元不超过1300元部分需缴纳5%的个人所得税．试写出月收入在800元到1300元之间的人应缴纳的税金y(元)和月收入x(元)之间的函数关系式．

4.今年植树节，同学们种的树苗高约1.80米．据介绍，这种树苗在10年内平均每年长高0.35米．求树高与年数之间的函数关系式．并算一算4年后同学们中学毕业时这些树约有多高．

3.仓库内原有粉笔400盒．如果每个星期领出36盒，求仓库内余下的粉笔盒数Q与星期数t之间的函数关系．

2.甲市到乙市的包裹邮资为每千克0.9元，每件另加手续费0.2元，求总邮资y(元)与包裹重量x(千克)之间的函数解析式，并计算5千克重的包裹的邮资．

1.已知y－3与x成正比例，且x＝2时，y＝7

(1)写出y与x之间的函数关系．

(2)y与x之间是什么函数关系．

(3)计算y＝－4时x的值．

一次函数、正比例函数以及它们的关系：

函数的解析式都是用自变量的一次整式表示的，我们称它们为一次函数(linear function)．一次函数通常可以表示为y＝kx+b的形式，其中k、b是常数，k≠0．

特别地，当b＝0时，一次函数y＝kx(常数k≠0)出叫正比例函数(direct proportional function)．正比例函数也是一次函数，它是一次函数的特例．

例1 下列函数关系中，哪些属于一次函数，其中哪些又属于正比例函数？

(1)面积为10cm²的三角形的底a(cm)与这边上的高h(cm)；

(2)长为8(cm)的平行四边形的周长L(cm)与宽b(cm)；

(3)食堂原有煤120吨，每天要用去5吨，x天后还剩下煤y吨；

(4)汽车每小时行40千米，行驶的路程s(千米)和时间t(小时)．

分析 确定函数是否为一次函数或正比例函数，就是看它们的解析式经过整理后是否符合y＝kx+b(k≠0)或y＝kx(k≠0)形式，所以此题必须先写出函数解析式后解答．

解 (1)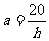，不是一次函数．

(2)L＝2b+16，L是b的一次函数．

(3)y＝150－5x，y是x的一次函数．

(4)s＝40t,s既是t的一次函数又是正比例函数．

例2 已知函数y＝(k－2)x+2k+1，若它是正比例函数，求k的值．若它是一次函数，求k的值．

分析 根据一次函数和正比例函数的定义,易求得k的值．

解 若y＝(k－2)x+2k+1是正比例函数,则2k+1＝0,即k＝．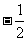

若y＝(k－2)x+2k+1是一次函数,则k－2≠0,即k≠2．

例3 已知y与x－3成正比例，当x＝4时，y＝3．

(1)写出y与x之间的函数关系式；

(2)y与x之间是什么函数关系；

(3)求x＝2.5时，y的值．

解 (1)因为 y与x－3成正比例,所以y＝k(x－3)．

又因为x＝4时，y＝3，所以3＝ k(4－3)，解得k＝3，

所以y＝3(x－3)＝3x－9．

(2) y是x的一次函数．

(3)当x＝2.5时，y＝3×2.5＝7.5．

例4 已知A、B两地相距30千米，B、C两地相距48千米．某人骑自行车以每小时12千米的速度从A地出发，经过B地到达C地．设此人骑行时间为x(时)，离B地距离为y(千米)．

(1)当此人在A、B两地之间时，求y与x的函数关系及自变量x取值范围．

(2)当此人在B、C两地之间时，求y与x的函数关系及自变量x的取值范围．

分析 (1)当此人在A、B两地之间时，离B地距离y为A、B两地的距离与某人所走的路程的差．

(2)当此人在B、C两地之间时，离B地距离y为某人所走的路程与A、B两地的距离的差．

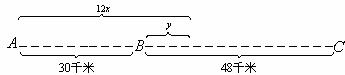
解 (1) y＝30－12x．(0≤x≤2.5)

(2) y＝12x－30．(2.5≤x≤6.5)

例5　某油库有一没储油的储油罐，在开始的8分钟时间内，只开进油管，不开出油管，油罐的进油至24吨后，将进油管和出油管同时打开16分钟，油罐中的油从24吨增至40吨．随后又关闭进油管，只开出油管，直至将油罐内的油放完．假设在单位时间内进油管与出油管的流量分别保持不变．写出这段时间内油罐的储油量y(吨)与进出油时间x(分)的函数式及相应的x取值范围．

分析 因为在只打开进油管的8分钟内、后又打开进油管和出油管的16分钟和最后的只开出油管的三个阶级中，储油罐的储油量与进出油时间的函数关系式是不同的，所以此题因分三个时间段来考虑．但在这三个阶段中，两变量之间均为一次函数关系．

解 在第一阶段：y＝3x(0≤x≤8)；

在第二阶段：y＝16+x(8≤x≤16)；

在第三阶段：y＝－2x+88(24≤x≤44)．