4.一次函数y＝3x+b的图象与两坐标轴围成的三角形面积是24，求b.

3.已知函数y＝2x-4.

(1)作出它的图象；

(2)标出图象与x轴、y轴的交点坐标；

(3)由图象观察，当-2≤x≤4时，函数值y的变化范围.

2.利用例3的图象，求汽车在高速公路上行驶4小时后，小明离北京的路程.

1.求下列直线与x轴和y轴的交点，并在同一直角坐标系中画出它们的图象.

(1)y＝4x-1；　　　　　 (2).

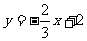2.在画实际问题中的一次函数图象时，要考虑自变量的取值范围，画出的图象往往不再是一条直线.

1.一次函数y＝kx+b,当x＝0时，y＝b；当y＝0时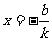，.所以直线y＝kx+b与y轴的交点坐标是(0,b),与x轴的交点坐标是；

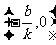例1 若直线y＝-kx+b与直线y＝-x平行，且与y轴交点的纵坐标为-2；求直线的表达式.

分析 直线y＝-kx+b与直线y＝-x平行，可求出k的值,与y轴交点的纵坐标为-2,可求出b的值.

解 因为直线y＝-kx+b与直线y＝-x平行，所以k＝-1,又因为直线与y轴交点的纵坐标为-2,所以b＝-2,因此所求的直线的表达式为y＝-x-2.

例2 求函数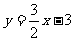与x轴、y轴的交点坐标，并求这条直线与两坐标轴围成的三角形的面积.

分析 求直线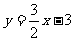与x轴、y轴的交点坐标，根据x轴、y轴上点的纵坐标和横坐标分别为0，可求出相应的横坐标和纵坐标；结合图象，易知直线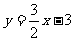与x轴、y轴围成的三角形是直角三角形，两条直角边就是直线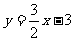与x轴、y轴的交点与原点的距离.

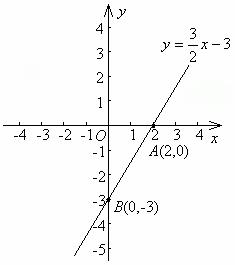
解 当y＝0时，x＝2，所以直线与x轴的交点坐标是A(2,0)；当x＝0时，y＝-3,所以直线与y轴的交点坐标是B(0，-3).

.

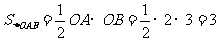例3 画出第一节课中问题(1)中小明距北京的路程s(千米)与在高速公路上行驶的时间t(时)之间函数s＝570-95t的图象.

分析 这是一题与实际生活相关的函数应用题，函数关系式s＝570-95t中，自变量t是小明在高速公路上行驶的时间，所以0≤t≤6,画出的图象是直线的一部分.再者，本题中t和s取值悬殊很大，故横轴和纵轴所选取的单位长不一致.

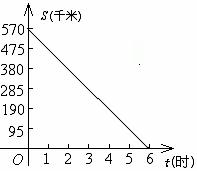
讨论 1.上述函数是否是一次函数？这个函数的图象是什么？

2.在实际问题中，一次函数的图象除了直线和本题的图形外，还有没有其他的情形？你能不能找出几个例子加以说明.

例4 旅客乘车按规定可以免费携带一定重量的行李．如果所带行李超过了规定的重量，就要按超重的千克收取超重行李费．已知旅客所付行李费y(元)可以看成他们携带的行李质量x(千克)的一次函数为．画出这个函数的图象，并求旅客最多可以免费携带多少千克的行李？

分析 求旅客最多可以免费携带多少千克的行李数，即行李费为0元时的行李数．为此只需求一次函数与x轴的交点横坐标的值．即当y＝0时，x＝30．由此可知这个函数的自变量的取值范围是x≥30．

解 函数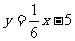(x≥30)图象为：

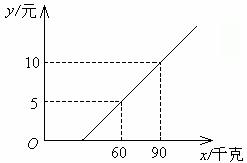
当y＝0时，x＝30.

所以旅客最多可以免费携带30千克的行李.

例5 今年入夏以来，全国大部分地区发生严重干旱．某市自来水公司为了鼓励市民节约用水，采取分段收费标准，若某户居民每月应交水费y(元)是用水量x(吨)的函数，当0≤x≤5时，y＝0.72x,当x＞5时，y＝0.9x-0.9．

(1)画出函数的图象；

(2)观察图象，利用函数解析式，回答自来水公司采取的收费标准.

分析 画函数图象时，应就自变量0≤x≤5和x＞5分别画出图象，当0≤x≤5时，是正比例函数，当x＞5是一次函数，所以这个函数的图象是一条折线.

解 (1)函数的图象是：

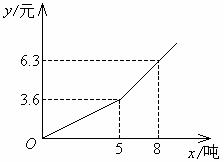
(2)自来水公司的收费标准是：当用水量在5吨以内时，每吨0.72元；当用水量在5吨以上时，每吨0.90元.

2.求直线y＝-2x-3与x轴和y轴的交点，并画出这条直线.

分析 x轴上点的纵坐标是0，y轴上点的横坐标0．由此可求x轴上点的横坐标值和y轴上点的纵坐标值．

解 因为x轴上点的纵坐标是0，y轴上点的横坐标0，所以当y＝0时，x＝-1.5，点(-1.5,0)就是直线与x轴的交点；当x＝0时，y＝-3，点(0，-3)就是直线与y轴的交点.

过点(-1.5,0)和(0，-3)所作的直线就是直线y＝-2x-3.

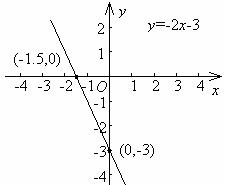
　 　所以一次函数y＝kx+b,当x＝0时，y＝b；当y＝0时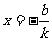，.所以直线y＝kx+b与y轴的交点坐标是(0,b),与x轴的交点坐标是.

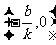1.在画函数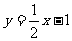的图象时，通过列表，可知我们选取的点是(0,-1)和(2,0)，这两点都在坐标轴上，其中点(0,-1)在y轴上，点(2,0)在x轴上，我们把这两个点依次叫做直线与y轴与x轴的交点.

4.在平面直角坐标系中,画出函数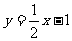的图象.我们画一次函数时,所选取的两个点有什么特征,通过观察图象,你发现这两个点在坐标系的什么地方?