
3、点M(x,5)在点A(0,2)和点B(-2,0)连接的直线上,则x=____________ 。
2、过点A(0,-2),且与直线y=5x平行的直线是( )
A、y=5x+2 B、y=5x―2
C、y=―5x+2 D、y=―5x-2
黑板分为左、中、右三部分,中间与右边用于教师板书课本例题等,写满后擦去更新,左边用于板书以下内容。
|
第四课时作业优化设计
1、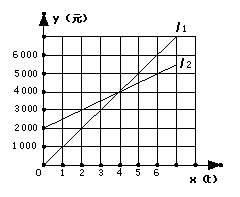 如下图,
如下图,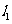 反映了某公司的销售收入与销售量的关系,
反映了某公司的销售收入与销售量的关系,
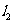 反映了该公司产品的销售成本与销售量的关系,当该公司赢利(收入大于成本)时,销售量(
)
反映了该公司产品的销售成本与销售量的关系,当该公司赢利(收入大于成本)时,销售量(
)
A、小于3t B、大于3t
C、小于4t D、大于4t
2、选用课时作业优化设计。
1、课本第48页习题18.3第9、10题。
2、用一次函数解析式解决实际问题时,要注意自变量的取值范围。
1、求一次函数的解析式往往用待定系数法,即根据题目中给出的两个条件确定一次函数解析式y=kx+b(k≠0)中两个待定系数k和b的值。
课本第47页练习第1、2题。
(二)解法归纳
教师讲解:通过上面三道题,我们基本上掌握了求一次函数y=kx+b(k≠0)的系数k与b的方法,这种先设待求函数关系式(其中含有未知的常数系数),再根据条件列出方程或方程组,求未知系数,从而得到结果的方法,叫做待定系数法。
待定系数法是一种应用广泛的数学方法,在代数式、方程等内容的“实践与探索”中,学生早已无意识地应用过。本节教学的主要目的不仅是方法的使用,还应突出这种方法所蕴含的数学思想:未知和已知、变量和常量的相互转化。作为待定系数法依据的是多项式恒等理论,不要对学生讲授,但教师应明确,并根据情况适当渗透。要提醒学生注意“已知函数的一组对应值”和“图象经过一个已知点”的作用。也要注意求得函数关系式后,对实际问题的解释和检验。
(一)通过实例总结方法
1、教师提出问题:已知一个一次函数中当自变量x=-2时,函数值y=-1,当x=3时,y=-3。请写出这个一次函数的解析式。
教师分析求解方法:根据一次函数的定义,可以设这个一次函数为y=kx+b(k≠0),问题就归结为如何求出k与b的值。
由已知条件可知x=-2时,y=-1,故有-1=-2k+b。
再由已知条件x=3时,y=-3,可得-3=3k+b。
由于两个条件都要满足,故可把k与b看作未知量,联立关于k、b的二元一次方程,
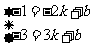 ,解得
,解得 ,再把所求得的k与b的值代回y=kx+b(k≠0),
,再把所求得的k与b的值代回y=kx+b(k≠0),
所以,一次函数解析式为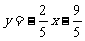 。
。
2、教师提出(例4):已知弹簧的长度y(厘米)在一定的限度内是所挂物体质量x(千克)的一次函数。现已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7.2厘米,求这个一次函数的关系式。
教师分析解法:已知y是x的函数,关系式是一次函数,故可设为y=kx+b(k≠0),所以要求的就是系数k和b的值。在这个问题中,不挂物体时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7.2厘米,就是已知条件x和y的两组对应值,也就是当x=0时,y=6;当x=4时,y=7.2。可以分别将它们代入函数式,转化为求k与b的二元一次方程组,进而求得k与b的值。
教师要求学生自己解题,学生解后教师给出答案:
设所求函数的关系式是y=kx+b(k≠0),由题意,得:
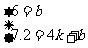 ,解这个方程组,得
,解这个方程组,得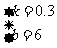 。
。
所以所求函数的关系式是 。(其中自变量有一定的范围)
。(其中自变量有一定的范围)
点拨:(1)本题中把两对函数值代入解析式后,把求解k和b的过程,转化为关于k和b的二元一次方程组的问题。(2)这个问题是与实际问题有关的函数,自变量往往有一定的范围。
3、教师提出问题:若一次函数y=mx-(m-2)过点(0,3),求m的值。
教师要求学生自行解题,对部分学生可作如下提示:考虑到直线 y=mx-(m-2)过点(0,3),说明点(0,3)在直线上,这里虽然已知条件中没有直接给出x和y的对应值,但由于图象上每一点的坐标(x,y)代表了函数的一对对应值,所以此题转化为已知x=0时,y=3,求m。即求关于m的一元一次方程3=-(m-2),解得m=-1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com