1.情境导入

　　 教师利用多媒体演示课本第54页图17.5.2(上节课的例题图象).

　　 对照图象,请同学们回答下列问题.

　　 (1)当x取何值时,2x-5=-x+1?

　　 (2)当x取何值时,2x-5>-x+1?

　　 (3)当x取何值时,2x-5<-x+1?

2.学会用图象法解一元一次方程和一元一次不等式.

1.了解一次函数与一元一次方程、一元一次不等式之间的相互关系.毛

(四)板书设计

(三)延伸拓展

　　 1.链接生活

　　 某果农准备把上市的60吨鲜水果从A地运往B地,经过调查得知:从A地到B地有汽­车和火车两种运输工具,两种线路的路程相同,均为s千米.在运输的过程中,除收取­每吨每小时5元的冷藏费外,其他费用如下表:

　　 ┌────┬─────┬──────┬───────┐

　　 │　　　　 │行驶速度　 │　 运输单价　 │　　　　　　　 │

　　 │运输工具│(千米/时) │(元/吨.千米)│装卸总费用(元)│

　　 ├────┼─────┼──────┼───────┤

　　 │　 汽车　 │　 50　　 │　　 2　　　 │　　 3000　　　 │

　　 ├────┼─────┼──────┼───────┤

　　 │　 火车　 │　 80　　 │　　 1.7　　 │　　 4620　　 　│

　　 └────┴─────┴──────┴───────┘

　　 (1)请分别写出利用汽车、火车运输这批水果所要的总费用y₁和y₂(用含s式­子表示);

　　 (2)为减少费用,请你帮助该果农设计出使费用较少的运输方案.

　　 2.实践探索

　　 (1)实践活动

　　 课后在相关网站上收集摄氏温度与华氏温度之间相互关系的资料和数据,并探­究这两种温度之间的函数关系.

　　 (2)巩固练习

　　 课本第57页习题17.5第4题和第5题.毛

(二)教学流程

　　 1.情境导入

　　 教师利用多媒体再次演示以前的幻灯片(课本第34页中“问题1”).

　　 请同学们在课本的图17.2.6中找出两个图象的交点坐标,讨论交流这个交点坐­标的实际意义,并说明小强出发多长时间后超过爷爷.

　　 2.课前热身

　　 回顾:前面,我们已经学习过函数的图象与坐标轴的交点坐标的求法,你能说说­具体的解题思路和方法吗?(学生讨论交流,举手回答)

　　 3.合作探究

　　 (1)整体感知

　　 从本节课开始,我们将利用三节课的时间,探讨利用已学的函数知识解决简单的­实际问题.本节课,我们着重探讨通过观察函数图象,解答提出的问题以及用图象法­解二元一次方程组的方法.

　　 (2)四边互动

　　 互动1

　　 师:利用多媒体演示幻灯片1.

　　 问题1:学校有一批复印任务,原来由甲复印社承接,按每100页40元计费.现乙复­印社表示:若学校先按月付给一定数额的承包费,则可按每100页15元收费.两复印社­每月收费情况如图所示.

　　 根据图象回答:

　　 (1)乙复印社的每月承包费是多少?

　　 (2)当每月复印多少页时,两复印社实际收费相同?

　　 (3)如果每月复印页数在1200页左右,那么应选择哪个复印社?

　　 师:请同学们分组讨论下列问题:

　　 (1)“收费相同”在图象上怎样反映出来?

　　 (2)如何在图象上看出函数值的大小?

　　 生:在小组内展开交流,各组推选代表发表所在小组的观点.

　　 师:请对照函数图象,独立解答问题1中提出的问题,然后在小组内交流自己的结­论.

　　 生:独立尝试,并在小组内交流自己的结论,反思完善自己的观点.

　　 明确　 由图象可知:横轴表示所要复印的页数,纵轴表示复印相应页数收取的费­用;两种“收费相同”是指在复印页数相同的情况下的费用相同,即在两个函数图象­上的横、纵坐标相同──两个图象的交点坐标;比较两个函数值的大小要看哪个图­象在上方(或下方),位于上方图象对应部分的函数值比位于下方对应部分的函数值­大.

　　 归纳可知:由函数图象解答问题时,首先要明确横、纵轴表示的含义,函数图象­的交点坐标表示两个图象上横、纵坐标都相同的点,在横轴上的一定取值范围内,位­于上方图象的函数值要比位于下方图象的函数值大.

　　 一般地,从函数图象上观察得出值是一个估计值,图象画得越准确,观察得越仔­细,所得的值就越准确.

　　 互动2

　　 师:利用多媒体演示幻灯片2.

　　 做一做:在课本17.3问题2中,小张的同学小王以前没有存过零用钱,听到小张在­存零用钱,表示从小张存款当月起每个月存22元,争取超过小张.请你在同一平面直­角坐标系中分别画出小张和小王存款和月份之间的函数关系的图象,在图上找一找­半年以后小王的存款能否超过小张?至少几个月后小王的存款能超过小张?

　　 请同学们简要介绍解题思路(步骤),然后在小组内交流.

　　 生:独立思考后,在小组内展开讨论交流.

　　 师:请同学们解答“做一做”中的问题,在小组内比较谁画出的图形较准确,谁­考虑的问题周到?

　　 生:动手操作,并讨论交流.

　　 明确　 首先应该根据题意求出两个函数关系式,再在同一个坐标系中画出这两­个函数的图象,最后通过观察函数图象解答问题.

　　 设从现在开始的月份数为x,则小张的存款数为:y=12x+50;小王的存款数为:y­=22x,画出的图象如图所示.

　　 由图象可知:小王半年后的存款超过小张(此时小王存款的图象上的点位于小张­存款图象上对应点的上方);至少要5个月后,小王的存款才能超过小张.

　　 思考:你能用代数的方法解答这个问题吗?试试看.

　　 互动3

　　 师:利用多媒体演示幻灯片3.

　　 例　 利用图象解方程组: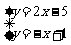

　　 师:(点拨)由前面探索的经验得出,两个函数图象的交点坐标,同时满足这两个­图象的方程,表明交点的坐标是联立两个图象方程组成的方程组的解.

　　 由此,你能想像出用图象法解方程组的一般步骤吗?请在讨论的基础上举手回答.

　　 生:讨论交流,逐个举手回答,达成共识.

　　 师:请尝试解答过程,然后同桌交流结果.

　　 生:动手操作,并交流解答的过程和结论.

　 　明确 　师生共同归纳解题的过程和结果,教师用多媒体演示.

　　 解:在直角坐标系中画出两条直线,如图所示.

　　 由图象观察可得:两条直线的交点坐标是(2,-1).

　　 所以方程组的解为

　　 4.达标反馈

　　 请解答课本第54页练习 第1题 第2题.

　　 (教师在教室里来回巡视,进行必要的指点和帮助)

　　 5.学习小结

　　 (1)内容总结

　　 本节课我们主要学习了哪些知识?

　　 (观察函数图象,解决简单问题;用图象法解二元一次方程组.)

　　 (2)方法归纳

　　 用图象法解二元一次方程组的过程是:首先画出两个函数的图象,再通过观察找­出图象交点的坐标,交点的坐标就是方程组的解.

(一)本课目标

　　 1.理解函数图象交点的意义.

　　 2.能够对照函数图象回答提出的问题.

　　 3.会用图象法解二元一次方程组.

第1课时

　　 3课时.

2.多媒体课件撷英

　　 (1)课件资讯

　　 利用Powerpoint制作幻灯片.

　　 (2)素材储备

　　 幻灯片1:问题1.幻灯片2;做一做.幻灯片3:例题.幻灯片4:问题2.幻灯片5:问题­3.