
(三)延伸拓展
1.链接生活
某次飞机表演,起飞后匀速2分钟到达500米高空,在原地5分钟完成规定的盘旋、翻转表演动作,然后用3分钟的时间匀速着陆.请选择适当的知识表示自飞机起飞到着陆过程中,飞机飞行的高度(米)与飞行时间(分)之间的关系.
(提示:用图象法表示)
2.实践探索
(1)实践活动
请同学们课后根据个人的实际,撰写一篇关于本章知识学习的心得体会.
(2)巩固练习
课本复习题第1题(在课本上写出选择的结果)第2题、第3题、第5题.
(2)四边互动
互动1
师:利用多媒体演示幻灯片1(不显示各个方框内的文字),请同学们概括归纳本章学习的主要知识结构,并在各个方框内填上适当的文字内容.
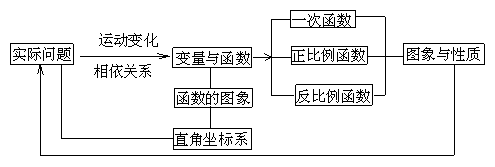
生:独立尝试,在小组内展开交流,然后举手回答.
明确 教师逐个点击方框,显示方框内容,验证学生回答的结论.
互动2
师:利用多媒体演示幻灯片2,请同学们归纳坐标系中点的坐标的主要特征.
(1)坐标轴上的点的坐标具有怎样的特征?
(2)象限内的点的坐标具有怎样的特征?
(3)关于x轴对称的两点的坐标具有怎样的特征?关于y轴、坐标系原点对称的两点呢?
生:逐个举手回答,不断补充完善.
明确 教师利用幻灯片演示结果,验证学生回答的结论.
互动3
师:利用多媒体演示幻灯片3(只显示表格的第一行和第一列文字).
|
函数名称 |
表达形式 |
图象特点 |
主要性质 |
|
一次函数 |
y=kx+b(k≠0) |
不与坐标轴平行的直线 |
当k>0时,随x的增大而增大;当k<0时, 随x的增大而减小 |
|
正比例函数 |
y=kx(k≠0) |
经过坐标系原点的直线 |
|
|
反比例函数 |
y=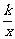 (k≠0) (k≠0) |
双曲线 |
(在同一个象限内) 与一次函数性质相 反 |
生:讨论交流,完成表格中的空格.
明确 教师利用多媒体演示:逐个点击表格中的空格,显示空格中的内容,验证学生操作的结果.
互动4
师:请同学们在讨论的基础上,概括归纳出如何确定函数的自变量的取值范围.并各举一例加以说明.
生:讨论交流,举手回答,不断补充完善,达成共识.
明确 师生共同归纳可得:当函数是自变量的整式时,函数自变量的取值范围是一切实数;当函数是自变量的分式(分母中含有自变量)时,必须使分母不为零;当函数是自变量的二次根式时,被开方数必须是非负数;在实际问题中,必须使实际有意义.
互动5
师:利用多媒体演示幻灯片4.
(1)若一次函数y=mx+2x-2中y随x的增大而增大,求m的取值范围.
答案:m>-2.
 (2)已知正比例函数y=kx中y随x的增大而减小,确定一次函数y=x-k的图象所经过的象限;
(2)已知正比例函数y=kx中y随x的增大而减小,确定一次函数y=x-k的图象所经过的象限;
答案:经过第一、三、四象限.
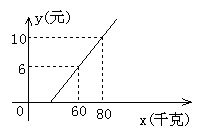
 (3)长途汽车客运公司规定旅客可以随身携带一定重量的行李,如果超过规定,则需要购买行李票,已知行李费用y(元)是行李重量x(千克)的一次函数,其图象如图所示,则y与x之间的函数关系式是 y=
(3)长途汽车客运公司规定旅客可以随身携带一定重量的行李,如果超过规定,则需要购买行李票,已知行李费用y(元)是行李重量x(千克)的一次函数,其图象如图所示,则y与x之间的函数关系式是 y=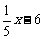 旅客可免费携带行李的重量范围是 不超过30千克.
旅客可免费携带行李的重量范围是 不超过30千克.
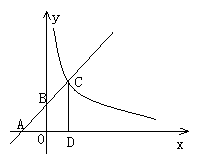
(4)如图所示,已知直线y=kx+b与坐标轴相交于点A、B,且与双曲线y=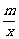 在第一象限交于点C,CD⊥x轴,垂足为D,若OA=OB=OD=1.求
在第一象限交于点C,CD⊥x轴,垂足为D,若OA=OB=OD=1.求
①点A、B、D的坐标;
②一次函数与反比例函数的解析式.
答案:①A(-1,0),B(0,1),D(1,0) ②y=x+1,y= .
.
生:独立尝试后,和同学交流讨论.
明确 教师利用多媒体演示各题的解答过程和结果,验证学生操作的结果.
求一次函数的解析式需要知道两点的坐标,求正比例和反比例函数的解析式只要知道一点的坐标,但不能是原点坐标.
4.达标反馈
(多媒体演示幻灯片5)

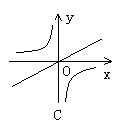
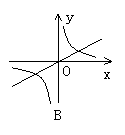
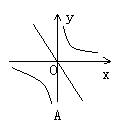 (1)函数y=kx,y=
(1)函数y=kx,y=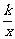 (k≠0)在同一坐标系中的图象大致是图中的(B)
(k≠0)在同一坐标系中的图象大致是图中的(B)
(2)直线y=kx+b经过点A(1,2),B(-1,-4),判断点C(2,5)是否在直线AB上,说明你的理由.
答案:点C在直线AB上,直线的解析式为y=3x-1,当x=2时y=5,故点(2,5)是直线y=3x-1上的点,则C在直线AB上.
5.学习小结
(1)内容总结
请同学们回顾一下,本节课我们主要复习了哪些内容?
(本章知识结构体系;坐标系的相关知识;三个常见函数的图形和性质)
(2)方法归纳
正确地理解和掌握函数的一般表达形式、函数图形特征和函数的性质是我们解决函数问题的关键.
(二)教学流程
1.复习导入
通过本章的学习,你学到了哪些主要知识?请简单地告诉我和同学们.
2.课前热身
学生在讨论交流的基础上,概括归纳本章所学的主要内容.
3.合作探究
(1)整体感知
本节课我们主要复习的内容可分为以下三个部分:
(一)本课目标
1.了解本章的知识结构体系.
2.了解平面直角坐标系的意义,了解坐标轴上点、象限点、对称点的坐标特征.
3.了解一次函数(正比例函数)和反比例函数的意义,掌握一次函数、反比例函数的图象特征和性质.
第1课时
2课时
2.多媒体课件撷英
(1)课件资讯
利用Powerpoint制作幻灯片.
(2)素材储备
幻灯片1:本章知识结构框图;幻灯片2:坐标系中特殊点的坐标的特征;幻灯片3:几个函数的归类表;幻灯片4:训练题1;幻灯片5:达标反馈1;幻灯片6:训练题2(函数解析式的求法);幻灯片7:训练题3(由图象解方程、不等式);幻灯片8:训练题4(利用函数解决问题);幻灯片9:达标反馈2.
1.教具学具准备
多媒体一台,投影仪一台,胶片若干;三角板一副,几何练习簿一本,铅笔、橡皮等.
2.课型及基本教学思路
课型:复习课.
教学思路:知识梳理──习题选讲──训练巩固──应用提高.
1.重点、难点
重点:一次函数、反比例函数的图象特征及其性质.
难点:利用一次函数的图象及其性质解决简单的实际问题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com