
3.已知一次函数y=kx+5的图象经过点(-1,2),则k= .
2.若函数y= -2xm+2是正比例函数,则m的值是 .
1.已知一个正比例函数的图象经过点(-2,4),则这个正比例函数的表达式是 .
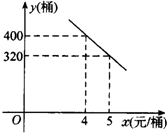
26.(12分)某校八年级(1)班共有学生50人,据统计原来每人每年用于购买饮料的平均支出是a元,经测算和市场调查,若该班学生集体改饮某品牌的桶装纯净水,则年总费用由两部分组成,一部分是购买纯净水的费用,另一部分是其他费用780元,其中纯净水的销售价x(元/桶)与年购买总量y(桶)之间满足如图所示关系.
(1)求y与x之间的函数关系式.
(2)若该班每年需要纯净水380桶,且a为120时,请你根据提供的信息分析一下,该班学生集体改饮桶装纯净水与个人买饮料,哪一种花钱更少?
25.(12分)为了学生的身体健康,学校课桌、凳的高度都是按一定的关系科学设计的,小明对学校所添置的一批课桌、凳进行观察研究,发现它们可以根据人的身长调长高度.于是,他测量了一套课桌,凳相应的四档高度,得到如下数据:
|
|
第一档 |
第二档 |
第三档 |
第四档 |
|
凳高x(cm) |
37.0 |
40.0 |
42.0 |
45.0 |
|
桌高y(cm) |
70.0 |
74.8 |
78.0 |
82.8 |
(1)小明经过对数据探究发现:桌高y是凳高x的一次函数,请你求出这个一次函数的关系式.(不要求写出x的取值范围)
(2)小明回家后,测量了家里的写字台和凳子,写字台的高度为77cm,凳子的高度为43.5cm,请你判断它们是否配套?说明理由.
24.(10分)甲、乙两家超市以相同的价格出售同样的商品,为吸引顾客,各自推出不同的优惠方案;甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价8.5折优惠,设顾客预计累计购物x元(x>300)
(1)请用含x的代数式分别表示顾客在两家超市购物所付的费用;
(2)试比较顾客到哪家超市购物更优惠?并说明你的理由.
23.(10分)某商场经营一批进价2元一件的小商品,在营销中发现此商品的销售单价与销售量之间的关系如下表:
|
单价(元) |
3 |
5 |
9 |
11 |
|
销售量(件) |
18 |
14 |
6 |
2 |
(1)一天中商场按表中最低价和最高价销售,分别获利多少元?
(2)猜测日销售量y与单价x之间的关系式.
(3)按(2)的关系式,求当这种商品单价为7元时的日销售量.
22.(8分)如图是一次函数y=-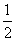 x+5图象的一部分,利用图象回答下列问题:
x+5图象的一部分,利用图象回答下列问题:
(1)求自变量的取值范围.
(2)在(1)在条件下,y是否有最小值?如果有就求出最小值;如果没有,请说明理由.
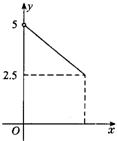
21.(8分)在平面直角坐标系xOy中,直线y=-x绕点O顺时针旋转90°得到直线L,直线L与反比例函数y=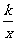 的图象的一个交点为A(a,3),试确定反比例函数的解析式.
的图象的一个交点为A(a,3),试确定反比例函数的解析式.
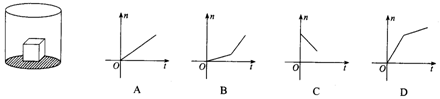
20.如图所示,在一个玻璃器中,放有一个正方形铁块,用同样的速度向容器注水,则下列函数的图象,能表示水面的高度h与注水时间t的关系式的是( )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com