11.汽车从距A站300千米的B站，以每小时60千米的速度开向A站，写出汽车离B站S(千米)与开出的时间t(时)之间的函数关系是_________ ，自变量t的取值范围是____________.

9. 如果一次函数y=(k+1)x+(b－2)的函数图象不经过第一象限，则k的范围是_________, b的范围是_________.

8. 已知函数y=(m－　2)x－2,要使函数值y随自变量x的增大而增大，则m取值范围是_________.

7.写出如图所示的直线解析式____________,

6.盛满10千克水的水箱，每小时流出0.5千克的水，写出水箱中的剩余水量y(千克)与时间t(时)之间的函数关系是_____________,自变量t的取值范围是________.

4.已知一个三角形的面积为1，一边的长为x，这边上的高为y ，则y关于x的函数关系式为__________，该函数图象在第__　　　　 __象限.

2.函数y=kx+3的图象过点(1，2)，则这个函数的解析式是_______.

1.点A(1，m)在函数y=2x的图象上，则A关于x轴的对称点的坐标是___．

(1)分别写出两厂的收费y(元)与印制数量x(份)之间的关系式；

(2)在同一直角坐标系中作出它们的图象；

(3)根据图象回答：印制800份宣传材料时，选择哪家印刷厂比较合算？

该公司拟拿出3000元用于印制宣传材料，找哪家印刷厂印制宣传材料能多一些？

§17.4－§17.5　一、1－3　ACB　4－5　ADD；二1、16，2、四，3、(1)100，(2)甲，(3)8米/秒；三、1、(1)x₀=1；(2)y = x+2,，2、(1)略，(2)；四、(1)S₁=6,(2)S₂=6,(3)面积为定值，(4)或；五、y =x+1500,y =2.5x,(2)略，(3)乙厂合算，甲厂多一些。

垂直x轴于点A，作BC垂直y轴于点C。

(1)　　 求长方形OABC的面积S₁；

(2)　　 作类似长方形OA₁B₁C₁，求长方形OA₁B₁C₁

的面积S₂；(3)你发现了什么？

(4)利用(3)的结论解决：在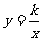的图象上有一点M，作MN垂直x轴于N点，MH垂直y轴于H，已知长方形ONMH面积为9，求解析式