P73　　 1、2、3。

2．相似三角形的识别

第一课时　 相似三角形的识别(一)

教学目标

3、如果一条直线平行于三角形一边，与其它两边或其延长线相交截得的三角形与原三角形相似吗?指出它们的对应边。

2．两个相似三角形的相似比为1，这两个三角形有什么关系?

1．填空。

　　 ＿＿＿＿＿＿＿的三角形叫做相似三角形。

判断下列两个三角形是否相似?简单说明理由，如果相似，写出对应边的比例

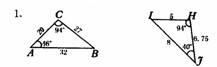
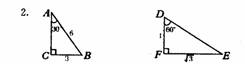
4．例：如果一个三角形的三边长分别是5、12、13，与其相似的三角形的最长．边是39，那么较大三角形的周长是多少?较小三角形与较大三角形的周长的比是多少?

分析：这两个三角形会相似，对应边是哪些边?相似比是多少?哪一个三角形较大?要计算出它的周长还需求什么?根据什么采求?

3．如果△ABC∽△A′B′C′，相似比K＝1，你会发现什么呢? ＝＝＝1，所以可得AB＝A′B′,BC＝B′C′，AC＝A′C′，因此这两个三角形不仅形状相同，且大小也相同，这样的三角形称之为全等三角形，全等三角形是相似三角形的特例，试问：

　　 全等的两个三角形一定相似吗?

　　 相似的两个三角形会全等吗?

　　 全等的符号与相似的符号之间有什么关系与区别?

2．△ABC中，D，E是AB、AC的中点，连结DE，那么△ADE与△ABC相似吗?为什么?如果相似，它们的相似比为多少?

　　 如果点D不是AB中点，是AB上任意一点，过D作DE∥BC，交AC边于E，那么△ADE与ABC是否也会相似呢?

　　 判断它们是否相似，由①对应角是否相等，②对应边是否成比例去考虑。能否得对应角相等?根据平行线性质与一个公共角可以推出①，而对应边是否成比例呢?目前还没有什么依据，同学们不妨用刻度尺量一量，算一算是否成比例?通过度量，计算发现＝＝．

所以可以判断出△ADE与△ABC会相似。　　

若是如图DE∥BC，与BA、CA延长线交于D、E，那么△ADE与△ABC还会相似吗?试一试看。如果相似写出它们对应边的比例式．

1．相似三角形的有关概念：

　　 由复习中引入，如果两个多边形的对应边成比例，对应角都相等，那么这两个多边形相似．

　　 三角形是最简单的多边形．由此可以说什么样的两个三角形相似?

如果两个三角形的三条边都成比例，三个角对应相等，那么这两个三角形相似，如在△ABC与△A′B′C′中，∠A＝A′，∠B＝∠B′，∠C＝∠C′＝＝ 那么△ABC与△A′B′C′相似，记作△ABC∽△A′B′C′；“∽”是表示相似的符号，读作“相似于”，这样两三角形相似就读作：“△ABC相似于△A′B′C′”。

由于∠A＝∠A′，∠B＝∠B′，∠C＝∠C′，所以点A的对应顶点是A′，B与B′是对应顶点，C与C′是对应顶点，书写相似时，通常把对应顶点写在对应位置上，以便比较容易找到相似三角形中的对应角、对应边．如果记＝＝＝K，那么这个K就表示这两个相似三角形的相似比．相似比就是它们的对应边的比，它有顺序关系．如△ABC∽△A′B′C′，它的相似比为K，即指＝K，那么△A′B′C′与△ABC的相似比应是，就不是K了，应为多少呢?同学们想一想?

　 　什么是相似形?识别两个多边形是否相似的标准是什么?