
第一节学习了利用相似三角形的知识来计算那些不能直接测量到的物体的高度或宽度,认识到数学知识在实践中是应用广泛的,本节课再学习相似三角形的另一个应用:等分线段。
2、会利用相似三角形的性质说明等分线段的原理。
教学过程
P82习题18、3 6
第二课时 相似三角形的应用(二)
教学目标
1、会把一已知线段几等分。
本节课学习应用相似三角形的性质,测量计算物体的高度,在应用时要分清转到数学上是哪两个三角形会相似,它们对应的边是哪一边,利用比例的性质求证答案。
2.在同一时刻物体的高度与它的影长成正比,在某一时刻,有人测得高为1.8米的竹竿的影长为3米,此时某高楼影长为60米,那么高楼的高度为多少米?
1.到操场上用例1的方法测量旗杆的高,并与同伙交流看看计算结果是否大致上一样。
第二题我们根据两个三角形相似,对应边成比例,列出比例式汁算出AB的长。人们从很早开始,就懂得应用这种方法来计算那些不能直接测量的物体的高度或宽度。
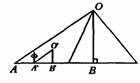 例1:古代的数学家想出了一种测量金字塔高度的方法:为了测量金字塔的高度OB,先竖一根已知长度的木棒O′B′,比较棒子的影长A′B′与金字塔的影长AB,即可近似算出金字塔的高度OB,如果O′B′=l,A′B′=2,AB=274,求金字塔的高度OB。
例1:古代的数学家想出了一种测量金字塔高度的方法:为了测量金字塔的高度OB,先竖一根已知长度的木棒O′B′,比较棒子的影长A′B′与金字塔的影长AB,即可近似算出金字塔的高度OB,如果O′B′=l,A′B′=2,AB=274,求金字塔的高度OB。
这实际上与上述问题是一样的。
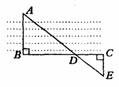 例2.我军一小分队到达某河岸,为了测量河宽,只用简单的工具,就可以很快计算河的宽度,在河对岸选定一个目标作为点A,再在河的这一岸上选点B和C,使AB⊥BC,然后选点E,使EC⊥BC,用眼睛测视确定BC和AE的交点D,此时如果测得BD=120米,DC=60米,EC=50米,就能算出两岸间的大致距离AB。
例2.我军一小分队到达某河岸,为了测量河宽,只用简单的工具,就可以很快计算河的宽度,在河对岸选定一个目标作为点A,再在河的这一岸上选点B和C,使AB⊥BC,然后选点E,使EC⊥BC,用眼睛测视确定BC和AE的交点D,此时如果测得BD=120米,DC=60米,EC=50米,就能算出两岸间的大致距离AB。
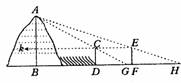 例3.我国魏晋时期的数学家刘徽的《海岛算经》中有一题:今有望海岛,立两表齐高三丈,前后相去千步,今后表与前表参相直,从前表却行一百二十三步,人目着地取望岛峰与表末参合,从后表却行一百二十七步,人目看地取望岛峰亦与表末参合,问岛高及去表各几何?画成图形,用现在话表述即是:要求海岛的山峰AB的高度,在D和F处都树立标杆DC和 FE,标杆高都是3丈,相隔1000步(一步等于5尺),并且AB、CD、EF在同一截面上。从标杆DC退后123步的G处,可看到山峰顶A和标杆顶C在一直线上;从标杆FE退后127步的H处,也可看到山峰顶A和标杆顶正在一直线上,求山高AB及它和标杆CD的水平距离BD。
例3.我国魏晋时期的数学家刘徽的《海岛算经》中有一题:今有望海岛,立两表齐高三丈,前后相去千步,今后表与前表参相直,从前表却行一百二十三步,人目着地取望岛峰与表末参合,从后表却行一百二十七步,人目看地取望岛峰亦与表末参合,问岛高及去表各几何?画成图形,用现在话表述即是:要求海岛的山峰AB的高度,在D和F处都树立标杆DC和 FE,标杆高都是3丈,相隔1000步(一步等于5尺),并且AB、CD、EF在同一截面上。从标杆DC退后123步的G处,可看到山峰顶A和标杆顶C在一直线上;从标杆FE退后127步的H处,也可看到山峰顶A和标杆顶正在一直线上,求山高AB及它和标杆CD的水平距离BD。
 1、相似三角形有哪些性质?
1、相似三角形有哪些性质?
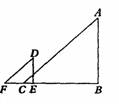
2.如图,B、C、E、F是在同一直线上,AB⊥BF,DE⊥BF,AC∥DF,
(1)∠DEF与∠ABC相似吗?为什么?
(2)若DE=1,EF=2,BC=10,那么AB等于多少?
P81 2、6
4、相似三角形的应用
第一课时 相似三角形的应用(一)
教学目标
会应用相似三角形的有关性质,测量简单的物体的高度或宽度。
教学过程
(填空形式,同学回答)相似三角形( )相等,( )的比等于相似比,面积的比等于( )。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com