
5.如图,三个正方形中的两个的面积S1=25,S2=144,则另一个的面积S3为________.
综合运用
u 认真解答,一定要细心哟!
4.在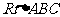 中,
中, 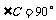 ,
,
(1)如果a=3,b=4,则c= ;
(2)如果a=6,b=8,则c= ;
(3)如果a=5,b=12,则c= ;
(4) 如果a=15,b=20,则c= .
3.一个直角三角形中,两直角边长分别为3和4,下列说法正确的是( )
 A.斜边长为25
B.三角形周长为25
A.斜边长为25
B.三角形周长为25
C.斜边长为5 D.三角形面积为20
2. △ABC的三条边长分别是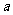 、
、 、
、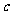 ,则下列各式成立的是( )
,则下列各式成立的是( )
A.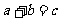 B.
B.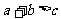 C.
C.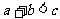 D.
D.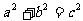
1. 下列说法正确的是( )
A.若 a、b、c是△ABC的三边,则a2+b2=c2
B.若 a、b、c是Rt△ABC的三边,则a2+b2=c2
C.若 a、b、c是Rt△ABC的三边,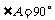 ,则a2+b2=c2
,则a2+b2=c2
D.若 a、b、c是Rt△ABC的三边,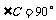 ,则a2+b2=c2
,则a2+b2=c2
2.关于勾股定理的证明方法有很多.赵爽的证法是一种面积证法,其中的依据是图形经过割补拼接后,只要没有重叠,没有空隙,面积不会改变.“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲。正因为此,这个图案被选为2002年在北京召开的世界数学家大会的会徽。
聚焦
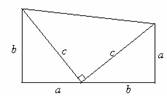 [例] 如图所示,可以利用两个全等的直角三角形拼出一个梯形.借助这个图形,你能用面积法来验证勾股定理吗?
[例] 如图所示,可以利用两个全等的直角三角形拼出一个梯形.借助这个图形,你能用面积法来验证勾股定理吗?
分析:面积法验证勾股定理关键是要找到一些特殊图形(如直角三角形,正方形,梯形)的面积之和等于另一些特殊图形的面积,从而达到验证的目的.
解:此图可以这样理解,有三个Rt△其面积分别为 ab,
ab, ab和
ab和 c2.还有一个直角梯形,其面积为
c2.还有一个直角梯形,其面积为 (a+b)(a+b).
(a+b)(a+b).
由图形可知: (a+b)(a+b)=
(a+b)(a+b)=  ab+
ab+ ab+
ab+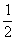 c2
c2
整理得(a+b)2=2ab+c2, a2+b2+2ab=2ab+c2, ∴ a2+b2=c2 .
由此得到勾股定理.
这正是美国第20任总统茄菲尔德证明勾股定理的方法.
双基淘宝
u 仔细读题,一定要选择最佳答案哟!
1.勾股定理:如果直角三角形的两直角边分别是a、b,斜边为c,那么a2+b2=c2.即直角三角形中两直角边的平方和等于斜边的平方.
18.1 勾股定理(1)
知识领航
23. BQ=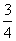 24.
24. 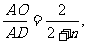 理由略。
理由略。
22.依题意可画示意图为:由题意知AM=25米,BC=20米,DE=50米,由BC∥DE知,△ABC∽ △ADE,从而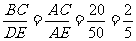 。又设河宽 MN=x米,故AM,AN分别为△ABC, △ADE的对应高线,从而
。又设河宽 MN=x米,故AM,AN分别为△ABC, △ADE的对应高线,从而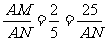 ,故AN=
,故AN=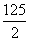 米,所以MN=AN-AM=
米,所以MN=AN-AM=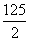 -25=
-25=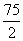 米,即河宽为
米,即河宽为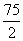 米。
米。
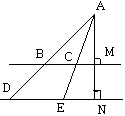 第22题图
第22题图
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com