
1.已知直角三角形中30°角所对的直角边长是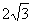 cm,则另一条直角边的长是( )
A. 4cm B.
cm,则另一条直角边的长是( )
A. 4cm B. 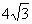 cm C. 6cm
D.
cm C. 6cm
D. 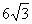 cm
cm
2.勾股定理的作用:(1)计算;(2)证明带有平方的问题;(3)实际应用.
聚焦
[例]甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源.为了不致于走散,他们用两部对话机联系,已知对话机的有效距离为15千米.早晨8:00甲先出发,他以6千米/时的速度向东行走,1小时后乙出发,他以5千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗?
分析:要求甲、乙两人的距离,就要确定甲、乙两人在平面的位置关系,由于甲往东、乙往北,所以甲所走的路线与乙所走的路线互相垂直,然后求出甲、乙走的路程,利用勾股定理,即可求得甲、乙两人的距离.
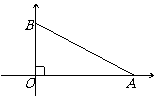 解:如图,甲从上午8:00到上午10:00一共走了2小时,
解:如图,甲从上午8:00到上午10:00一共走了2小时,
走了12千米,即OA=12.
乙从上午9:00到上午10:00一共走了1小时,
走了5千米,即OB=5.
在Rt△OAB中,AB2=122十52=169,∴AB=13,
因此,上午10:00时,甲、乙两人相距13千米.
∵15>13, ∴甲、乙两人还能保持联系.
答:上午10:00甲、乙两人相距13千米,两人还能保持联系.
双基淘宝
u 仔细读题,一定要选择最佳答案哟!
1.在直角三角形中,若已知任意两边,就可以运用勾股定理求出第三边.无直角时,可作垂线构造直角三角形.
18.1 勾股定理(2)
知识领航
1.D 2.B 3.C
4.5; 10; 13;
25 5.169 6.中空正方形的面积为 ,也可表示为
,也可表示为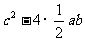 ,∴
,∴ =
=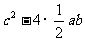 ,整理得
,整理得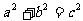 . 7.100m2 8.(1)分两种情况:当4为直角边长时,第三边长为5;当4为斜边长时,第三边长为
. 7.100m2 8.(1)分两种情况:当4为直角边长时,第三边长为5;当4为斜边长时,第三边长为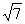 .(2)略 9.28cm 10.∵ 四边形BCC′D′为直角梯形,∴S梯形BCC′D′=
.(2)略 9.28cm 10.∵ 四边形BCC′D′为直角梯形,∴S梯形BCC′D′=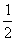 (BC+C′D′)·BD′=
(BC+C′D′)·BD′=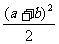 .∵Rt△ABC≌Rt△AB′C′, ∴∠BAC=∠BAC′. ∴∠CAC′=∠CAB′+∠B′AC′=∠CAB′+∠BAC=90°. ∴S梯形BCC′D′=S△ABC+S△CAC′+S△D′AC′=
.∵Rt△ABC≌Rt△AB′C′, ∴∠BAC=∠BAC′. ∴∠CAC′=∠CAB′+∠B′AC′=∠CAB′+∠BAC=90°. ∴S梯形BCC′D′=S△ABC+S△CAC′+S△D′AC′= 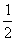 ab+
ab+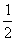 c2+
c2+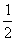 ab=
ab=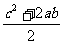 . ∴
. ∴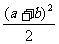 =
=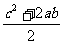 . ∴a2+b2=c2.
. ∴a2+b2=c2.
10.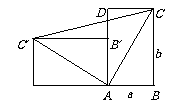 一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的验证方法.如图,火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连接CC′,设AB=a,BC=b,AC=c,请利用四边形BCC′D′的面积验证勾股定理:a2+b2=c2.
一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的验证方法.如图,火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连接CC′,设AB=a,BC=b,AC=c,请利用四边形BCC′D′的面积验证勾股定理:a2+b2=c2.
|
|||
|
答案:18.1 勾股定理(1)
9.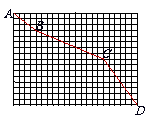 蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)
蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)
拓广创新
u 试一试,你一定能成功哟!
7. 如图,小李准备建一个蔬菜大棚,棚宽4m,高3m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,请计算阳光透过的最大面积.
如图,小李准备建一个蔬菜大棚,棚宽4m,高3m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,请计算阳光透过的最大面积.
6.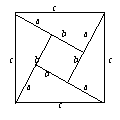 利用四个全等的直角三角形可以拼成如图所示的图形,这个图形被称为弦图.观察图形,验证:c2=a2+b2.
利用四个全等的直角三角形可以拼成如图所示的图形,这个图形被称为弦图.观察图形,验证:c2=a2+b2.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com