
7.已知等腰梯形ABCD的中位线EF的长为6,腰AD的长为5,则等腰梯形的周长为( ).
A.11 B.16 C.17 D.22
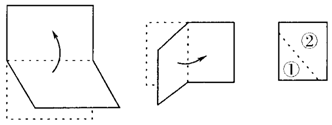
6.将一张矩形纸对折再对折(如图),然后沿着图中的虚线剪下,得到①,②两部分,将①展开后得到的平面图形是( ).
A.三角形 B.矩形 C.菱形 D.梯形
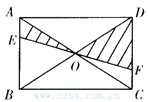
5.如图3,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形面积的( ).
A.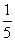 B.
B.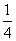 C.
C.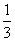 D.
D.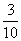
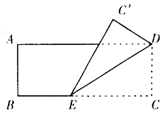
4.如图2,将一张矩形纸片ABCD那样折起,使顶点C落在C′处,其中AB=4,若∠C′ED=30°,则折痕ED的长为( ).
A.4
B.4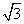 C.5
C.5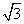 D.8
D.8
3.已知四边形ABCD是平行四边形,下列结论中,错误的是( ).
A.AB=CD; B.AC=BD; C.当AC⊥BD时,它是菱形; D.当∠ABC=90°时,它是矩形
2.下列说法中,正确的是( ).
A.等腰梯形的对角线互相垂直 B.菱形的对角线相等
C.矩形的对角线互相垂直; D.正方形的对角线互相垂直且相等
1.如图1,用两个完全相同的直角三角板,不能拼成下列图形的是( ).
A.平行四边形 B.矩形 C.等腰三角形 D.梯形
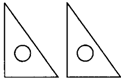
(1) (2) (3)
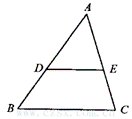
15.如图,若已知△ABC中,D、E分别为AB、AC的中点,则可得DE∥BC,且DE=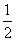 BC.根据上面的结论:
BC.根据上面的结论:
(1)你能否说出顺次连结任意四边形各边中点,可得到一个什么特殊四边形?并说明理由.
(2)如果将(1)中的“任意四边形”改为条件是“平行四边形”或“菱形”或“矩形”或“等腰梯形”,那么它们的结论又分别怎样呢?请说明理由.
附加题(10分)
如图,以△ABC的三边为边在BC的同侧分别作三个等边三角形,即△ABD、△BCE、△ACF,请回答下列问题,并说明理由.
(1)四边形ADEF是什么四边形?
(2)当△ABC满足什么条件时,四边形ADEF是矩形?
(3)当△ABC满足什么条件时,以A、D、E、F为顶点的四边形不存在.
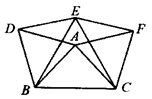
14.如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由?
(2)当点O运动何处时,四边形AECF是矩形?并说出你的理由.
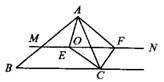
13.如图,一块正方形地板由全等的正方形瓷砖铺成,这地板的两条对角线上的瓷砖全是黑色,其余的瓷砖是白色的,如果有101块黑色瓷砖,那么瓷砖的总数是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com