3．　 培养学生的推理论证能力和逻辑思维能力．

2．　 能综合运用平行四边形的性质解决平行四边形的有关计算问题，和简单的证明题．

1．　 理解平行四边形中心对称的特征，掌握平行四边形对角线互相平分的性质．

19.1.1 平行四边形的性质(二)

3．如图，AD∥BC，AE∥CD，BD平分∠ABC，求证AB=CE．

2．在ABCD中，如果EF∥AD，GH∥CD，EF与GH相交与点O，那么图中的平行四边形一共有(　　 )．

(A)4个 (B)5个　 (C)8个　 (D)9个

1．(选择)在下列图形的性质中，平行四边形不一定具有的是(　　 )．

(A)对角相等 (B)对角互补 (C)邻角互补 (D)内角和是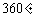

2．如图4.3－9，在ABCD中，AC为对角线，BE⊥AC，DF⊥AC，E、F为垂足，求证：BE＝DF．

1．填空：

(1)在ABCD中，∠A=，则∠B=　　 度，∠C=　　 度，∠D=　　 度．

(2)如果ABCD中，∠A-∠B=240，则∠A=　 度，∠B=　 度，∠C=　 度，∠D=　 度．

(3)如果ABCD的周长为28cm，且AB：BC=2∶5，那么AB= 　　cm，BC=　　 cm，CD=　　 cm，CD=　　 cm．

例1(教材P93例1)

　　 例2(补充)如图，在平行四边形ABCD中，AE=CF，

求证：AF=CE．

分析：要证AF=CE，需证△ADF≌△CBE，由于四边形ABCD是平行四边形，因此有∠D=∠B ，AD=BC，AB=CD，又AE=CF，根据等式性质，可得BE=DF．由“边角边”可得出所需要的结论．

证明略．