
2.会初步运用矩形的概念和性质来解决有关问题.
1.掌握矩形的概念和性质,理解矩形与平行四边形的区别与联系.
19.2.1 矩形(一)
3.已知:如图,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.
2.(填空)已知:△ABC中,点D、E、F分别是△ABC三边的中点,如果△DEF的周长是12cm,那么△ABC的周长是 cm.
1. (填空)一个三角形的周长是135cm,过三角形各顶点作对边的平行线,则这三条平行线所组成的三角形的周长是
cm.
(填空)一个三角形的周长是135cm,过三角形各顶点作对边的平行线,则这三条平行线所组成的三角形的周长是
cm.
3.如图,△ABC中,D、E、F分别是AB、AC、BC的中点,
(1)若EF=5cm,则AB= cm;若BC=9cm,则DE= cm;
(2)中线AF与DE中位线有什么特殊的关系?证明你的猜想.
2. 已知:三角形的各边分别为8cm 、10cm和12cm ,求连结各边中点所成三角形的周长.
已知:三角形的各边分别为8cm 、10cm和12cm ,求连结各边中点所成三角形的周长.
1.(填空)如图,A、B两点被池塘隔开,在AB外选一点C,连结AC和BC,并分别找出AC和BC的中点M、N,如果测得MN=20 m,那么A、B两点的距离是 m,理由是 .
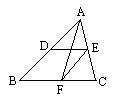
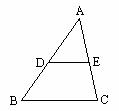 例1(教材P98例4) 如图,点D、E、分别为△ABC边AB、AC的中点,求证:DE∥BC且DE=
例1(教材P98例4) 如图,点D、E、分别为△ABC边AB、AC的中点,求证:DE∥BC且DE=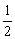 BC.
BC.
 分析:所证明的结论既有平行关系,又有数量关系,联想已学过的知识,可以把要证明的内容转化到一个平行四边形中,利用平行四边形的对边平行且相等的性质来证明结论成立,从而使问题得到解决,这就需要添加适当的辅助线来构造平行四边形.
分析:所证明的结论既有平行关系,又有数量关系,联想已学过的知识,可以把要证明的内容转化到一个平行四边形中,利用平行四边形的对边平行且相等的性质来证明结论成立,从而使问题得到解决,这就需要添加适当的辅助线来构造平行四边形.
方法1:如图(1),延长DE到F,使EF=DE,连接CF,由△ADE≌△CFE,可得AD∥FC,且AD=FC,因此有BD∥FC,BD=FC,所以四边形BCFD是平行四边形.所以DF∥BC,DF=BC,因为DE=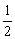 DF,所以DE∥BC且DE=
DF,所以DE∥BC且DE=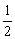 BC.
BC.
(也可以过点C作CF∥AB交DE的延长线于F点,证明方法与上面大体相同)
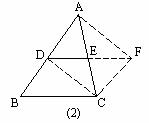 方法2:如图(2),延长DE到F,使EF=DE,连接CF、CD和AF,又AE=EC,所以四边形ADCF是平行四边形.所以AD∥FC,且AD=FC.因为AD=BD,所以BD∥FC,且BD=FC.所以四边形ADCF是平行四边形.所以DF∥BC,且DF=BC,因为DE=
方法2:如图(2),延长DE到F,使EF=DE,连接CF、CD和AF,又AE=EC,所以四边形ADCF是平行四边形.所以AD∥FC,且AD=FC.因为AD=BD,所以BD∥FC,且BD=FC.所以四边形ADCF是平行四边形.所以DF∥BC,且DF=BC,因为DE=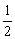 DF,所以DE∥BC且DE=
DF,所以DE∥BC且DE=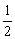 BC.
BC.
定义:连接三角形两边中点的线段叫做三角形的中位线.
[思考]:
(1)想一想:①一个三角形的中位线共有几条?②三角形的中位线与中线有什么区别?
(2)三角形的中位线与第三边有怎样的关系?
(答:(1)一个三角形的中位线共有三条;三角形的中位线与中线的区别主要是线段的端点不同.中位线是中点与中点的连线;中线是顶点与对边中点的连线. (2)三角形的中位线与第三边的关系:三角形的中位线平行与第三边,且等于第三边的一半.)
三角形中位线的性质:三角形的中位线平行与第三边,且等于第三边的一半.
[拓展]利用这一定理,你能证明出在设情境中分割出来的四个小三角形全等吗?(让学生口述理由)
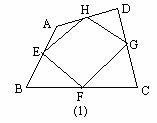
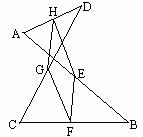
例2(补充)已知:如图(1),在四边形ABCD中,E、F、G、H分别是 AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
 分析:因为已知点E、F、G、H分别是线段的中点,可以设法应用三角形中位线性质找到四边形EFGH的边之间的关系.由于四边形的对角线可以把四边形分成两个三角形,所以添加辅助线,连接AC或BD,构造“三角形中位线”的基本图形后,此题便可得证.
分析:因为已知点E、F、G、H分别是线段的中点,可以设法应用三角形中位线性质找到四边形EFGH的边之间的关系.由于四边形的对角线可以把四边形分成两个三角形,所以添加辅助线,连接AC或BD,构造“三角形中位线”的基本图形后,此题便可得证.
证明:连结AC(图(2)),△DAG中,
∵ AH=HD,CG=GD,
∴ HG∥AC,HG=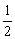 AC(三角形中位线性质).
AC(三角形中位线性质).
同理EF∥AC,EF=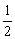 AC.
AC.
∴ HG∥EF,且HG=EF.
∴ 四边形EFGH是平行四边形.
此题可得结论:顺次连结四边形四条边的中点,所得的四边形是平行四边形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com