
3.已知:矩形ABCD中,BC=2AB,E是BC的中点,求证:EA⊥ED.
2. 在直角三角形ABC中,∠C=90°,AB=2AC,求∠A、∠B的度数.
在直角三角形ABC中,∠C=90°,AB=2AC,求∠A、∠B的度数.
1.(选择)矩形的两条对角线的夹角为60°,对角线长为15cm,较短边的长为( ).
(A)12cm (B)10cm (C)7.5cm (D)5cm
3.已知:如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,求∠AEO的度数.
2.(选择)
(1)下列说法错误的是( ).
(A)矩形的对角线互相平分 (B)矩形的对角线相等
(C)有一个角是直角的四边形是矩形 (D)有一个角是直角的平行四边形叫做矩形
(2)矩形的对角线把矩形分成的三角形中全等三角形一共有( ).
 (A)2对 (B)4对 (C)6对 (D)8对
(A)2对 (B)4对 (C)6对 (D)8对
1.(填空)
(1)矩形的定义中有两个条件:一是 ,二是 .
(2)已知矩形的一条对角线与一边的夹角为30°,则矩形两条对角线相交所得的四个角的度数分别为 、 、 、 .
(3)已知矩形的一条对角线长为10cm,两条对角线的一个交角为120°,则矩形的边长分别为 cm, cm, cm, cm.
例1 (教材P104例1)已知:如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4cm,求矩形对角线的长.
分析:因为矩形是特殊的平行四边形,所以它具有对角线相等且互相平分的特殊性质,根据矩形的这个特性和已知,可得△OAB是等边三角形,因此对角线的长度可求.
解:∵ 四边形ABCD是矩形,
∴ AC与BD相等且互相平分.
∴ OA=OB.
又 ∠AOB=60°,
∴ △OAB是等边三角形.
∴ 矩形的对角线长AC=BD = 2OA=2×4=8(cm).
 例2(补充)已知:如图 ,矩形
ABCD,AB长8 cm ,对角线比AD边长4 cm.求AD的长及点A到BD的距离AE的长.
例2(补充)已知:如图 ,矩形
ABCD,AB长8 cm ,对角线比AD边长4 cm.求AD的长及点A到BD的距离AE的长.
分析:(1)因为矩形四个角都是直角,因此矩形中的计算经常要用到直角三角形的性质,而此题利用方程的思想,解决直角三角形中的计算,这是几何计算题中常用的方法.
略解:设AD=xcm,则对角线长(x+4)cm,在Rt△ABD中,由勾股定理: ,解得x=6. 则 AD=6cm.
,解得x=6. 则 AD=6cm.
(2)“直角三角形斜边上的高”是一个基本图形,利用面积公式,可得到两直角边、斜边及斜边上的高的一个基本关系式: AE×DB= AD×AB,解得 AE= 4.8cm.
例3(补充) 已知:如图,矩形ABCD中,E是BC上一点,DF⊥AE于F,若AE=BC. 求证:CE=EF.
分析:CE、EF分别是BC,AE等线段上的一部分,若AF=BE,则问题解决,而证明AF=BE,只要证明△ABE≌△DFA即可,在矩形中容易构造全等的直角三角形.
证明:∵ 四边形ABCD是矩形,
 ∴ ∠B=90°,且AD∥BC.
∴ ∠1=∠2.
∴ ∠B=90°,且AD∥BC.
∴ ∠1=∠2.
∵ DF⊥AE, ∴ ∠AFD=90°.
∴ ∠B=∠AFD.又 AD=AE,
∴ △ABE≌△DFA(AAS).
∴ AF=BE.
∴ EF=EC.
此题还可以连接DE,证明△DEF≌△DEC,得到EF=EC.
3.再次演示平行四边形的移动过程,当移动到一个角是直角时停止,让学生观察这是什么图形?(小学学过的长方形)引出本课题及矩形定义.

矩形定义:有一个角是直角的平行四边形叫做矩形(通常也叫长方形).
矩形是我们最常见的图形之一,例如书桌面、教科书的封面等都有矩形形象.
[探究]在一个平行四边形活动框架上,用两根橡皮筋分别套在相对的两个顶点上(作出对角线),拉动一对不相邻的顶点,改变平行四边形的形状.
① 随着∠α的变化,两条对角线的长度分别是怎样变化的?
② 当∠α是直角时,平行四边形变成矩形,此时它的其他内角是什么样的角?它的两条对角线的长度有什么关系?

 操作,思考、交流、归纳后得到矩形的性质.
操作,思考、交流、归纳后得到矩形的性质.
矩形性质1 矩形的四个角都是直角.
矩形性质2 矩形的对角线相等.
如图,在矩形ABCD中,AC、BD相交于点O,由性质2有AO=BO=CO=DO=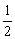 AC=
AC=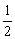 BD.因此可以得到直角三角形的一个性质:直角三角形斜边上的中线等于斜边的一半.
BD.因此可以得到直角三角形的一个性质:直角三角形斜边上的中线等于斜边的一半.
2.思考:拿一个活动的平行四边形教具,轻轻拉动一个点,观察不管怎么拉,它还是一个平行四边形吗?为什么?(动画演示拉动过程如图)
1.展示生活中一些平行四边形的实际应用图片(推拉门,活动衣架,篱笆、井架等),想一想:这里面应用了平行四边形的什么性质?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com