
2.理解并掌握菱形的定义及性质1、2;会用这些性质进行有关的论证和计算,会计算菱形的面积.
1.掌握菱形概念,知道菱形与平行四边形的关系.
19.2.2 菱形(一)
2.在Rt△ABC中,∠C=90°,AB=2AC,求∠A、∠B的度数.
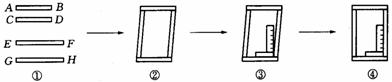
1.工人师傅做铝合金窗框分下面三个步骤进行:
⑴ 先截出两对符合规格的铝合金窗料(如图①),使AB=CD,EF=GH;
⑵ 摆放成如图②的四边形,则这时窗框的形状是 形,根据的数学道理是: ;
⑶ 将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是 形,根据的数学道理是:
;
2.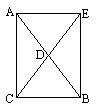 已知:如图 ,在△ABC中,∠C=90°, CD为中线,延长CD到点E,使得
DE=CD.连结AE,BE,则四边形ACBE为矩形.
已知:如图 ,在△ABC中,∠C=90°, CD为中线,延长CD到点E,使得
DE=CD.连结AE,BE,则四边形ACBE为矩形.
1.(选择)下列说法正确的是( ).
(A)有一组对角是直角的四边形一定是矩形(B)有一组邻角是直角的四边形一定是矩形
(C)对角线互相平分的四边形是矩形 (D)对角互补的平行四边形是矩形
例1(补充)下列各句判定矩形的说法是否正确?为什么?
(1)有一个角是直角的四边形是矩形; (×)
(2)有四个角是直角的四边形是矩形; (√)
(3)四个角都相等的四边形是矩形; (√)
(4)对角线相等的四边形是矩形; (×)
(5)对角线相等且互相垂直的四边形是矩形; (×)
(6)对角线互相平分且相等的四边形是矩形; (√)
(7)对角线相等,且有一个角是直角的四边形是矩形; (×)
(8)一组邻边垂直,一组对边平行且相等的四边形是矩形;(√)
(9)两组对边分别平行,且对角线相等的四边形是矩形. (√)
指出:
(l)所给四边形添加的条件不满足三个的肯定不是矩形;
(2)所给四边形添加的条件是三个独立条件,但若与判定方法不同,则需要利用定义和判定方法证明或举反例,才能下结论.
 例2 (补充)已知
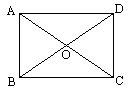
例2 (补充)已知  ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,AB=4 cm,求这个平行四边形的面积.
ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,AB=4 cm,求这个平行四边形的面积.
分析:首先根据△AOB是等边三角形及平行四边形对角线互相平分的性质判定出ABCD是矩形,再利用勾股定理计算边长,从而得到面积值.
解:∵ 四边形ABCD是平行四边形,
∴ AO=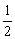 AC,BO=
AC,BO=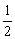 BD.
BD.
∵ AO=BO,
∴ AC=BD.
∴  ABCD是矩形(对角线相等的平行四边形是矩形).
ABCD是矩形(对角线相等的平行四边形是矩形).
在Rt△ABC中,
∵ AB=4cm,AC=2AO=8cm,
∴ BC=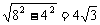 (cm).
(cm).
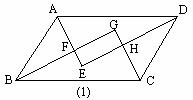
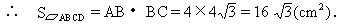
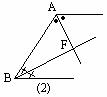
例3 (补充) 已知:如图(1), ABCD的四个内角的平分线分别相交于点E,F,G,H.求证:四边形EFGH是矩形.
ABCD的四个内角的平分线分别相交于点E,F,G,H.求证:四边形EFGH是矩形.
分析:要证四边形EFGH是矩形,由于此题目可分解出基本图形,如图(2),因此,可选用“三个角是直角的四边形是矩形”来证明.
 证明:∵ 四边形ABCD是平行四边形,
证明:∵ 四边形ABCD是平行四边形,
∴ AD∥BC.
∴ ∠DAB+∠ABC=180°.
又 AE平分∠DAB,BG平分∠ABC ,
∴ ∠EAB+∠ABG=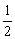 ×180°=90°.
×180°=90°.
∴ ∠AFB=90°.
同理可证 ∠AED=∠BGC=∠CHD=90°.
∴ 四边形EFGH是平行四边形(有三个角是直角的四边形是矩形).
4.事例引入:小华想要做一个矩形像框送给妈妈做生日礼物,于是找来两根长度相等的短木条和两根长度相等的长木条制作,你有什么办法可以检测他做的是矩形像框吗?看看谁的方法可行?
通过讨论得到矩形的判定方法.
矩形判定方法1:对角钱相等的平行四边形是矩形.
矩形判定方法2:有三个角是直角的四边形是矩形.
(指出:判定一个四边形是矩形,知道三个角是直角,条件就够了.因为由四边形内角和可知,这时第四个角一定是直角.)
3.矩形与平行四边形有什么共同之处?有什么不同之处?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com