1．若菱形的边长等于一条对角线的长，则它的一组邻角的度数分别为　　　　　　　 ．

例1　(补充) 已知：如图，四边形ABCD是菱形，F是AB上一点，DF交AC于E．

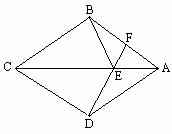　求证：∠AFD=∠CBE．

证明：∵　四边形ABCD是菱形，

∴　 CB=CD， CA平分∠BCD．

∴　 ∠BCE=∠DCE．又 CE=CE，

∴　 △BCE≌△COB(SAS)．

∴　 ∠CBE=∠CDE．

∵　在菱形ABCD中，AB∥CD， ∴∠AFD=∠FDC

∴　∠AFD=∠CBE．

　　 例2 (教材P108例2)略

　　 本节课安排了两个例题，例1是一道补充题，是为了巩固菱形的性质；例2是教材P108中的例2，这是一道用菱形知识与直角三角形知识来求菱形面积的实际应用问题．此题目，除用以巩固菱形性质外，还可以引导学生用不同的方法来计算菱形的面积，以促进学生熟练、灵活地运用知识．

3．难点的突破方法：

(1)课堂上演示由平行四边形改变成菱形．使学生对平行四边形与菱形的关系形成深刻的印象；

　(2)讲解这个定义时，要抓住概念的本质，应突出两条：①强调菱形是平行四边形；②一组邻边相等．另外还需指出定义既是判定又是性质．

(3)菱形的性质，可以让学生动手利用折纸、剪切的方法，探究、归纳．

方法一：将一张长方形的纸横对折，再竖对折(如教材P107的探究)，然后沿图中的虚线剪下，打开即是菱形纸片；

方法二：如图1，两张等宽的纸条交叉重叠在一起，重叠的部分ABCD就是菱形；

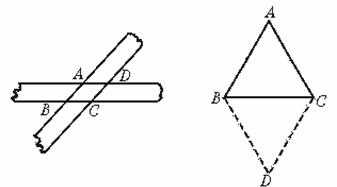
　　 图1　　　　　　　　　　 图2

方法三：将一张长方形纸对折，再在折痕上取任意长为底边，剪一个等腰三角形，然后打开即是菱形(如图2) ．

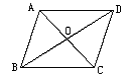(3)要让学生知道性质1的已知：如图，菱形ABCD，和结论：AB=BC=CD=DA．

性质2的已知：如图，在菱形ABCD中，对角线AC、BD相交于点O，和结论：AC⊥BD，AC平分∠BAD和∠BCD；BD平分∠ABC和∠ADC．并能灵活运用．

(4)指出：菱形是轴对称图形，它有两条对称轴，这两条对称轴是菱形的对角线，所以两条对称轴互相垂直．

(5)让学生知道：菱形ABCD被对角线AC、BD分成了四个全等的直角三角形，在计算或证明时常用这个结论．

(6)菱形的面积公式是 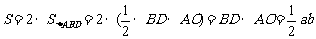(其中a、b是菱形的两条对角线分别的长)．即：“菱形的面积等于它的两条对角线长的积的一半”．还要指出：当不易求出对角线长时，就用平行四边形面积的一般计算方法计算菱形面积S=底×高．

2．教学难点：菱形的性质及菱形知识的综合应用．

1．教学重点：菱形的性质1、2．

4．根据平行四边形与矩形、菱形的从属关系，通过画图向学生渗透集合思想．

3．通过运用菱形知识解决具体问题，提高分析能力和观察能力．