1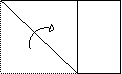．做一做：用一张长方形的纸片(如图所示)折出一个正方形．

学生在动手做中对正方形产生感性认识，并感知正方形与矩形的关系．问题：什么样的四边形是正方形？

正方形定义：有一组邻边相等并且有一个角是直角的平行四边形叫做正方形．

指出：正方形是在平行四边形这个大前提下定义的，其定义包括了两层意：

(1)有一组邻边相等的平行四边形 (菱形)

(2)有一个角是直角的平行四边形 (矩形)

本节课安排了三个例题，例1是教材P111的例4，例2与例3都是补充的题目．其中例1与例2是正方形性质的应用，在讲解时，应注意引导学生能正确的运用其性质．例3是正方形判定的应用，它是先判定一个四边形是矩形，再证明一组邻边，从而可以判定这个四边形是正方形．随后可以再做一组判断题，进行练习巩固(参看随堂练习1)，为了活跃学生的思维，也可以将判断题改为下列问题让学生思考：

①对角线相等的菱形是正方形吗？为什么？

②对角线互相垂直的矩形是正方形吗？为什么？

③对角线垂直且相等的四边形是正方形吗？为什么？如果不是，应该加上什么条件？

④能说“四条边都相等的四边形是正方形”吗？为什么？

⑤说“四个角相等的四边形是正方形”对吗？

3．难点的突破方法：

本节的主要内容是正方形概念、性质和判定方法．重点是正方形定义．

正方形学生在小学阶段已有初步了解，生活中应用很广，其时正方形不仅是特殊的平行四边形，而且是特殊的矩形，和特殊的菱形，学好正方形有助于巩固矩形、菱形各自特有的性质和判定．

学生在小学学过了正方形，他们知道正方形的四个角都是直角，四条边相等，正方形的面积等于它的边长的平方，本节课的教学是加深学生的理论认识，拓宽学生的知识面，如何使学生理解为什么正方形的四个角都是直角，四条边相等，拓宽了正方形对角线性质的知识．在教学中可以让学生动手从一张矩形纸中折出一个正方形，培养学生实践能力．另外，通过对正方形定义和性质的讲解，培养学生类比思想、归纳思想、转化思想和隔离方法．

(1)掌握正方形定义是学好本节的关键．正方形是在平行四边形的前提下定义的，它包含两层意思：

①有一组邻边相等的平行四边形 (菱形)

②有一个角是直角的平行四边形 (矩形)

正方形不仅是特殊的平行四边形，并且是特殊的矩形，又是特殊的菱形．教学时要结合教科书中P110中的图19.2－14，具体说明正方形与矩形、菱形的关系．这些关系是教学的一个难点，也是教学内容的重点和关键，要结合图形或者教具，或用简单的集合关系图，使学生把正方形与平行四边形、矩形、菱形的关系搞清楚．这些概念重叠交错，不易搞清楚，在教学这些内容时进度可稍放慢些．

(2)因为正方形是平行四边形、矩形，又是菱形，所以它的性质是它们性质的综合，不仅有平行四边形的所有性质，也有矩形和菱形的特殊性质，所以讲正方形性质的关键是在复习矩形、菱形的基础上进行总结．可以将正方形的性质总结如下：

边：对边平行，四边相等；

角：四个角都是直角；

对角线：对角线相等，互相垂直平分，每条对角线平分一组对角．

还要让学生注意到：正方形的一条对角线把正方形分成两个全等的等腰直角三角形，对角线与边的夹角是45°；正方形的两条对角线把它分成四个全等的等腰直角三角形，这是正方形的特殊性质．要使学生熟悉这些最基本的内容．

(3)对于怎样判定一个四边形是正方形，因为层次比较多，不必分析的太具体，只要强调能判定一个四边形是矩形，又能判定这个矩形也是菱形，或者先判定四边形是菱形，再判定这个菱形也是矩形，就可以判定这个四边形是正方形，实际上就是根据正方形定义来判定．

(4)正方形的性质和判定是本大节讲的平行四边形、菱形、矩形的性质与判定的综合．可以通过本节的教学总结、归纳前面所学的内容．还可以通过本节的教学，澄清学生存在的一些模糊概念．

2．教学难点：正方形与矩形、菱形的关系及正方形性质与判定的灵活运用．　

1．教学重点：正方形的定义及正方形与平行四边形、矩形、菱形的联系．　

2．理解正方形与平行四边形、矩形、菱形的联系和区别，通过正方形与平行四边形、矩形、菱形的联系的教学对学生进行辩证唯物主义教育，提高学生的逻辑思维能力．　

1．掌握正方形的概念、性质和判定，并会用它们进行有关的论证和计算．

19.2.3 正方形

3．做一做：

设计一个由菱形组成的花边图案．花边的长为15 cm，宽为4 cm，由有一条对角线在同一条直线上的四个菱形组成，前一个菱形对角线的交点，是后一个菱形的一个顶点．画出花边图形．　

2．已知：如图，M是等腰三角形ABC底边BC上的中点，DM⊥AB，EF⊥AB，ME⊥AC，DG⊥AC．求证：四边形MEND是菱形．