
19.3 .1 梯形(一)
3.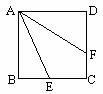 已知:如图,正方形ABCD中,E为BC上一点,AF平分∠DAE交CD于F,求证:AE=BE+DF.
已知:如图,正方形ABCD中,E为BC上一点,AF平分∠DAE交CD于F,求证:AE=BE+DF.
2.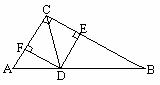 已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.求证:四边形CFDE是正方形.
已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.求证:四边形CFDE是正方形.
1.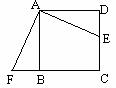 已知:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且DE=BF.
已知:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且DE=BF.
求证:EA⊥AF.
4.如图,E为正方形ABCD内一点,且△EBC是等边三角形,
求∠EAD与∠ECD的度数.
3. 已知:如图,四边形ABCD为正方形,E、F分别
为CD、CB延长线上的点,且DE=BF.
求证:∠AFE=∠AEF.
2.下列说法是否正确,并说明理由.
①对角线相等的菱形是正方形;( )
②对角线互相垂直的矩形是正方形;( )
③对角线垂直且相等的四边形是正方形;( )
 ④四条边都相等的四边形是正方形;(
)
④四条边都相等的四边形是正方形;(
)
⑤四个角相等的四边形是正方形.( )
1.正方形的四条边____ __,四个角___ ____,两条对角线____ ____.
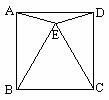
例1(教材P111的例4) 求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形.
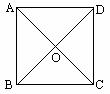 已知:四边形ABCD是正方形,对角线AC、BD相交于点O(如图).
已知:四边形ABCD是正方形,对角线AC、BD相交于点O(如图).
求证:△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形.
证明:∵ 四边形ABCD是正方形,
∴ AC=BD, AC⊥BD,
AO=CO=BO=DO(正方形的两条对角线相等,并且互相垂直平分).
∴ △ABO、△BCO、△CDO、△DAO都是等腰直角三角形,
并且 △ABO ≌△BCO≌△CDO≌△DAO.
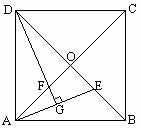 例2 (补充)已知:如图,正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F.
例2 (补充)已知:如图,正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F.
求证:OE=OF.
分析:要证明OE=OF,只需证明△AEO≌△DFO,由于正方形的对角线垂直平分且相等,可以得到∠AOE=∠DOF=90°,AO=DO,再由同角或等角的余角相等可以得到∠EAO=∠FDO,根据ASA可以得到这两个三角形全等,故结论可得.
证明:∵ 四边形ABCD是正方形,
∴ ∠AOE=∠DOF=90°,AO=DO(正方形的对角线垂直平分且相等).
又 DG⊥AE, ∴ ∠EAO+∠AEO=∠EDG+∠AEO=90°.
∴ ∠EAO=∠FDO.
∴ △AEO ≌△DFO.
∴ OE=OF.
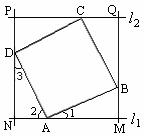 例3 (补充)已知:如图,四边形ABCD是正方形,分别过点A、C两点作l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB、DN分别交l2于Q、P点.
例3 (补充)已知:如图,四边形ABCD是正方形,分别过点A、C两点作l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB、DN分别交l2于Q、P点.
求证:四边形PQMN是正方形.
分析:由已知可以证出四边形PQMN是矩形,再证△ABM≌△DAN,证出AM=DN,用同样的方法证AN=DP.即可证出MN=NP.从而得出结论.
证明:∵ PN⊥l1,QM⊥l1,
∴ PN∥QM,∠PNM=90°.
∵ PQ∥NM,
∴ 四边形PQMN是矩形.
∵ 四边形ABCD是正方形
∴ ∠BAD=∠ADC=90°,AB=AD=DC(正方形的四条边都相等,四个角都是直角).
∴ ∠1+∠2=90°.
又 ∠3+∠2=90°, ∴ ∠1=∠3.
∴ △ABM≌△DAN.
∴ AM=DN. 同理 AN=DP.
∴ AM+AN=DN+DP
即 MN=PN.
∴ 四边形PQMN是正方形(有一组邻边相等的矩形是正方形).
2.[问题]正方形有什么性质?
由正方形的定义可以得知,正方形既是有一组邻边相等的矩形,又是有一个角是直角的菱形.
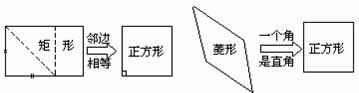
所以,正方形具有矩形的性质,同时又具有菱形的性质.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com